Πανεπιστήμιο Κρήτης
Τμήμα Επιστήμης και Τεχνολογίας Υλικών

Ποιος, που, πότε διδάσκει

Θεωρία: Κάθε Τρίτη 11-12 και Πέμπτη 11-1 στην αίθουσα 1 κτιρίου Φυσικής ο Γιάννης Ρεμεδιάκης, γραφείο B207 κτίριο ΤΕΥ.

Ασκήσεις: Κάθε Τρίτη 12-1 στην αίθουσα 1 κτιρίου Φυσικής ο Χαράλαμπος Μαβίδης (Ε-Mail: mavidis [at] iesl [dot] forth [dot] gr).
Ώρες γραφείου:
Στο ΙΤΕ (STEP-C, Κτίριο Α, Ισόγειο, Γραφείο 102): Τετάρτη 4μμ-6μμ (ή κατόπιν συνεννοήσεως μέσω e-mail)

Τρόπος βαθμολογίας

Η ύλη του μαθήματος και ο τρόπος βαθμολογίας θα είναι σχεδόν ίδια με πέρσι. Δείτε την σύντομη περιγραφή της ύλης, της βιβλιογραφίας και του τρόπου εξέτασης. Οι διαφορές είναι ότι (α) δεν υπάρχουν ασκήσεις για το σπίτι και (β) φέτος μετράνε στον βαθμό και τα 5 διαγωνίσματα και δεν επιτρέπονται απουσίες εκτός από πάρα πολύ σοβαρό λόγο. Αν ένας από τους 5 βαθμούς είναι πολύ μεγαλύτερος ή πολύ μικρότερος από τους άλλους 4 δεν θα μετρήσει στον μέσο όρο.

Διόρθωση 21/10/13: η ώρα των διαγωνισμάτων αλλάζει από 10 σε 11.

Τα διαγωνίσματα θα δίνονται Πέμπτη 11 το πρωί. Ξεκινάνε ακριβώς, όχι 11:15 και δεν επιτρέπεται αποχώρηση πριν το τέλος. Οι ημερομηνίες των διαγωνισμάτων είναι:

• 24/10/2013
• 14/11/2013
• 28/11/2013
• 19/12/2013
• 16/1/2014

Να επισκέπτεστε συχνά την σελίδα, οι ημερομηνίες ίσως αλλάξουν αν υπάρξει κάποιο έκτακτο γεγονός.

Η μέθοδος της διαστατικής ανάλυσης

• Οι διαστάσεις (μονάδες) ενός φυσικού μεγέθους γράφονται με μοναδικό τρόπο σαν συνάρτηση των θεμελιωδών διαστάσεων. Στο σύστημα SI, αυτές είναι πέντε: το μήκος (L), η μάζα (Μ), o χρόνος (T), το ηλεκτρικό φορτίο (Q) και η θερμοκρασία (T).
• Διαστατικά ανεξάρτητα μεγέθη είναι εκείνα των οποίων οι μονάδες δεν συνδέονται. Πχ η ενέργεια, ταχύτητα και μάζα δεν είναι ανεξάρτητα, αφού οι μονάδες [Ε]=[m][u]² (πχ στο SI J=kg (m/s)²). Αντίθετα, τα μεγέθη ενέργεια, ταχύτητα και μήκος είναι διαστατικά ανεξάρτητα.
• Θεώρημα: Από διαστατικά ανεξάρτητα φυσικά μεγέθη υπάρχει ένας και μόνο συνδυασμός που έχει δεδομένες μονάδες.
• Δείτε το άρθρο της wikipedia και τη σελ. 15 του βιβλίου "Κβαντομηχανική Ι" του Σ. Τραχανά.

Τι είναι η ΦΣΚ; Η απλή θεωρία της γραμμικής απόκρισης.

Αν σε κάποιο υλικό επιδράσουμε με κάποιο πεδίο, το υλικό είτε θα μεταβάλλει κάποια ιδιότητά του είτε θα εμφανίσει μια νέα ιδιότητα που δεν την είχε απουσία του πεδίου. Παραδείγματα: (1) Ζεσταίνω ένα υλικό (αλλάζω τη θερμοκρασία του κατά ΔΤ) και αλλάζει ο όγκος του κατά ΔV. (2) Τοποθετώ μια ηλεκτρική τάση, V στα άκρα του υλικού και αυτό διαρρέεται από ρεύμα, I. Οι αλλαγή της ιδιότητας του υλικού ή η νέα ιδιότητα που εμφανίστηκε (ΔV, I) λέγεται απόκριση.

Αν το εξωτερικό πεδίο είναι ασθενές, η απόκριση είναι ανάλογη του αιτίου που την προκάλεσε. Αυτό λέγεται θεωρία της γραμμικής απόκρισης. Η σταθερά αναλογίας είναι συνήθως ανάλογη του μεγέθους (μάζα ή όγκο ή μήκος κλπ) του υλικού και ανάλογη μιας εντατικής ιδιότητας του υλικού. Η τελευταία λέγεται συνάρτηση απόκρισης. Στα παραπάνω παραδείγματα πχ ισχύουν ο νόμος της διαστολής, ΔV=αVΔΤ, όπου α ο συντελεστής διαστολής και ο νόμος του Ohm, Ι=V/R=σ(A/L)V όπου σ η αγωγιμότητα του υλικού. Τα α και σ είναι δυο μόνο από τις πάμπολλες συναρτήσεις απόκρισης ενός υλικού.

Σκοπός της ΦΣΚ είναι να προσδιορίσει τις συναρτήσεις απόκρισης και να προτείνει τρόπους πειραματικού προσδιορισμού τους ή θεωρητικού υπολογισμού τους. Ιδιαίτερο ενδιαφέρον για τη ΦΣΚ έχει η ενοποίηση διαφορετικών φαινομένων η οποία εκφράζεται μέσω σχέσεων που συνδέουν διαφορετικές συναρτήσεις απόκρισης. Για παράδειγμα, η σχέση του Grüneisen συνδέει τον συντελεστή διαστολής με την θερμοχωρητικότητα και το υδροστατικό μέτρο ελαστικότητας.

Σε αυτό το μάθημα θα γνωρίσουμε αντιπροσωπευτικές συναρτήσεις απόκρισης σε μηχανικά, θερμικά, ηλεκτρικά και μαγνητικά πεδία και θα προσδιορίσουμε τις τιμές τους και τις θεωρητικές σχέσεις μεταξύ τους με δυο απλά μοντέλα. Σε πολλές περιπτώσεις θα συζητήσουμε και πειραματικές τεχνικές.

Περιοδικότητα και κρυσταλλική δομή

Η δομή των κρυσταλλικών στερεών καλύπτεται στο κεφ. 13 του βιβλίου του Ε. Ν. Οικονόμου. Χάρη στην ευγενική προσφορά των ΠΕΚ, μπορείτε να το πάρετε σε pdf από εδώ.

Περιοδικές συναρτήσεις σε 1D και 3D. Πλέγματα Bravais, Θεμελιώδης κυψελίδα, κυψελίδα Wigner-Seitz, μοναδιαία κυψελίδα.

Μελέτη της δομής fcc: ορισμοί και τάξη μεγέθους των d, z, V_i, n_i, ρ_M και εφαρμογή στον Cu.

Μελέτη της δομής fcc: ορισμοί και τάξη μεγέθους των r_i, R, f, n, r_s και εφαρμογή στον Cu.

(κεφ. 2) Ποσότητες που δείχνουν πόσο πυκνό είναι ένα στερεό

• Η απόσταση γειτόνων, d, είναι η μικρότερη μή μηδενική απόσταση μεταξύ ατόμων σε ένα στερεό. Τα άτομα που απέχουν d λέγονται πρώτοι γείτονες.
• Ο αριθμός σύνταξης, z, είναι ο αριθμός πρώτων γειτόνων ενός ατόμου.
• Ο όγκος ανά άτομο, V_i είναι ο συνολικός όγκος διαιρεμένος με τον αριθμό των ατόμων: V_i=V/N_i.
• Η συγκέντρωση ατόμων, n_i είναι ο αριθμός ατόμων ανά όγκο: n_i=N_i/V.
• Η πυκνότητα, ρ_M, είναι η μάζα του υλικού ανά όγκο: ρ_M=Μ/V.
• Η ακτίνα ιόντος, R, είναι η ακτίνα που θα είχε ένα άτομο αν στο στερεό δεν υπήρχε καθόλου αλληλοεπικάλυψη μεταξύ γειτονικών ατόμων: R=d/2.
• Η ακτίνα ιόντος, r_i είναι η ακτίνα που θα είχε ένα άτομο αν στο στερεό δεν υπήρχε καθόλου κενό ανάμεσα στα άτομα: 4/3πr_i³=V_i.
• Η πλήρωση, f, είναι το κλάσμα του χώρου που καταλαμβάνεται από άτομα εάν δεν υπήρχε καθόλου αλληλοεπικάλυψη μεταξύ γειτονικών ατόμων: f=N_i 4/3πR³/V.
• Η συγκέντρωση ηλεκτρονίων, n, είναι ο αριθμός ηλεκτρονίων (σθένους) ανά όγκο: n=N/V.
• Η ακτίνα ηλεκτρονίου (ή ακτίνα Wigner-Seitz), r_s, είναι η ακτίνα του χώρου που αντιστοιχεί σε ένα ηλεκτρόνιο αν στο στερεό δεν υπήρχε καθόλου κενό ανάμεσα στα άτομα: 4/3πr_s³=V/N.

Oι παραπάνω ποσότητες αποτελούν μέτρο του πόσο πυκνό είναι ένα υλικό, και συνδέονται μεταξύ τους με προφανείς σχέσεις. Γνωρίζοντας μια από τις d, V_i, n_i, ρ_M, r_i, R, n, r_s για ένα στερεό μπορώ να υπολογίσω εύκολα οποιαδήποτε άλλη. Θα χρησιμοποιήσω βέβαια και σταθερές από τον περιοδικό πίνακα (σθένος, ζ, ατομικό βάρος, A, κρυσταλλική δομή κλπ).

Κρυσταλλική δομή=πλέγμα και βάση. Διανύσματα πλέγματος και βάσης δομής fcc στην θεμελιώδη και μοναδιαία κυψελίδα. Κάποια πλέγματα Bravais (sc, bcc, fcc, hex, bct) και κάποιες χαρακτηριστικές κρυσταλλικές δομές (diamond, ZnS, wurtzite, graphite, hcp). Σύγκριση δομών fcc και hcp. Συντεταγμένες διανυσμάτων πλέγματος και ατόμων βάσης στην δομή hcp.

Μετά από πολλές διαμαρτυρίες για την ώρα των διαγωνισμάτων, αυτή τροποποιείται ως εξής: Τα διαγωνίσματα θα δίνονται Πέμπτες 11-12 (την πρώτη ώρα του μαθήματος). Η χαμένη ώρα θα αναπληρώνεται την επόμενη εβδομάδα. Επομένως την Πέμπτη 31/10/13 θα κάνουμε τρίωρο 10-1.

Κανόνες διαγωνισμάτων:

• Κάθε διαγώνισμα αφορά μόνο ύλη που διδάχτηκε στο διάστημα μεταξύ αυτού και του προηγούμενου διαγωνίσματος. Εξαίρεση αποτελεί η ύλη του διαγωνίσματος 1 (διαστατική ανάλυση και υπολογισμός ποσοτήτων σχετικών με την πυκνότητα, (d, r_s, V_i κλπ), τα οποία θα πρέπει να τα ξέρετε καλά σε όλο το μάθημα.
• Τα διαγωνίσματα διαρκούν μια ακαδημαϊκή ώρα. Πρέπει να είστε στη θέση σας 11 ακριβώς (όχι 11.15).
• Nα έχετε μαζί σας κομπιουτεράκι. Δεν επιτρέπεται να δανειστείτε κομπιουτεράκι από διπλανό σας. Κινητά και οποιαδήποτε άλλη ηλεκτρονική συσκευή απαγορεύονται.
• Να έχετε ταυτότητα ή άλλο δημόσιο έγγραφο με φωτογραφία.
• Δεν επιτρέπεται αποχώρηση πριν τη λήξη της εξέτασης.

H δομή hcp (διανύσματα πλέγματος, θέσεις ατόμων βάσης, μήκη και γωνίες δεσμών, αριθμός σύνταξης). Η ιδανική δομή hcp. Υπολογισμός των d, z, V_i, n_i, ρ_M, r_i, R, f, n, r_s για hcp. Αριθμητικές τιμές για Re και Τi.

Κατηγορίες στερεών και είδη δεσμών (ανάλογα με το είδος των ηλεκτρονίων σθένους των ατόμων τους):

• Mηδέν ηλεκτρόνια (ευγενή αέρια, συνήθη μοριακά στερεά): κυριαρχούν οι ελκτικές αλληλεπιδράσεις Van der Waals, με αποτέλεσμα δομές πυκνής διάταξης όπως η fcc (z=12).
• Ένα ή δυο ηλεκτρόνια (απλά μέταλλα): Τα ηλεκτρόνια μοιράζονται σε όλο το στερεό όπως υπαγορεύει η κβαντομηχανική. Και πάλι προτιμώνται πυκνές δομές όπως fcc, hcp (z=12). Σε στερεά με μικρά άτομα, οι δομές fcc/hcp θα έδιναν μεγάλες συγκεντρώσεις ηλεκτρονίων οι οποίες θα αύξαναν πολύ την κινητική ενέργεια λόγω της κβαντομηχανικής αντίστασης στον εντοπισμό (σκεφτείτε την αρχή του Heisenberg). Έτσι, συχνά προτιμώνται δομές με λίγο μικρότερη πλήρωση, όπως η bcc (z=8).
• Τρία έως επτά ηλεκτρόνια(μονωτές, ημιαγωγοί): Είναι η πιο περίπλοκη κατηγορία. Εκτός από τον ανταγωνισμό μεταξύ ηλεκτρομαγνητισμού (που θέλει όσο γίνεται πιο πυκνές δομές) και κβαντομηχανικής (που θέλει όσο γίνεται πιο αραιές δομές), εδώ υπάρχει και η κατευθυντικότητα των δεσμών η οποία οφείλεται στο είδος των ηλεκτρονίων σε p τροχιακά. Στην κατηγορία αυτή συναντάμε δομές με αριθμούς σύνταξης 4 (διαμάντι) ή 6 (NaCl). Ωστόσο, υπάρχουν και δομές με αριθμούς σύνταξης εκτός αυτού του εύρους, όπως το γραφένιο (z=3) και το CsCl (z=8).
• Εννέα και περισσότερα ηλεκτρόνια(μεταβατικά μέταλλα): εδώ υπάρχει ανταγωνισμός μεταξύ των s ηλεκτρονίων που προσπαθούν να κάνουν δομές πυκνής διάταξης (πχ fcc Cu, z=12), και των d ηλεκτρονίων που επιθυμούν συγκεκριμένες γωνίες δεσμών (πχ bcc Fe, z=8).

Για περισσότερες λεπτομέρειες, δείτε το κεφ. 1.1 από το βιβλίο του Ε. Καξίρα.

1o διαγώνισμα. Αποτελέσματα

(κεφ. 13). Θεώρημα Bloch: Αν η δυναμική ενέργεια είναι περιοδική συνάρτηση, τότε οι λύσεις της εξίσωσης Schrodinger περιγράφονται από τρεις κβαντικούς αριθμούς που σχηματίζουν ένα κυματάνυσμα k και ισχύει ψ_k(r+R)= e^ik.R ψ_k(r), όπου R διάνυσμα του σχετικού πλέγματος Bravais.

Μια προφανής συνέπεια του θεωρήματος Βloch είναι ότι η πυκνότητα πιθανότητας |ψ|² είναι περιοδική συνάρτηση, άρα το ηλεκτρόνιο που περιγράφεται από την ψ είναι πλήρως απεντοπισμένο σε ολόκληρο το στερεό. Αυτό ισχύει σε όλα τα στερεά, είτε είναι μέταλλα, είτε είναι μονοτές.

Τα τέλεια κρυσταλλικά μέταλλα δεν έχουν αντίσταση, καθώς τα ηλεκτρόνια είναι πλήρως απεντοπισμένα και μπορούν να κινηθούν ακόμα και με την απειροελάχιστη ηλεκτρική τάση. Η αντίσταση οφείλεται σε ατέλειες (είτε χημικές, είτε δομικές) και στην θερμική κίνηση των ατόμων. Σε σχετικά καλά δείγματα, η θερμική κίνηση είναι πολύ πιο σημαντική, οπότε η ειδική αντίσταση σε θερμοκρασία δωματίου είναι συνήθως ανάλογη της απόλυτης θερμοκρασίας, ρ ~ Τ (παράδειγμα).

Μια δεύτερη συνέπεια του θεωρήματος Bloch είναι ότι τα κυματανύσματα k και k+G, όπου e^iG.R=1 για κάθε R του πλέγματος, περιγράφουν ακριβώς την ίδια φυσική κατάσταση. Είναι εύκολο να δείξει κανείς ότι το σύνολο των G αποτελεί πλέγμα Bravais. Αυτό το πλέγμα ονομάζεται αντίστροφο πλέγμα. Προφανώς, το αντίστροφο του αντιστρόφου είναι το ίδιο το πλέγμα.

Ας δούμε πρώτα τι γίνεται σε μια διάσταση. Εδώ το πλέγμα Bravais είναι μια σειρά σημείων σε θέσεις R=0, R=a, R=2a, R=-a, R=-2a κλπ, δηλαδή R=na όπου n ακέραιος και a το διάνυσμα πλέγματος. Το σύνολο των G για τα οποία e^iGR=1 για κάθε R είναι προφανώς οι αριθμοί G=0, G=2π/a, G=-2π/a κλπ, δηλαδή G=m 2π/a όπου m ακέραιος και 2π/a το διάνυσμα του αντιστρόφου πλέγματος. Αρκεί λοιπόν να μελετήσω τις καταστάσεις ηλεκτρονίων σε μια περίοδο. Μια επιλογή είναι η κυψελίδα Wigner-Seitz, δηλαδή το σύνολο των σημείων που είναι κοντύτερα στο 0 από ότι σε οποιοδήποτε άλλο σημείο του πλέγματος. Αυτή είναι η περιοχή -a/2<x<a/2 για το ευθύ πλέγμα και -π/a<k<π/a για το αντίστροφο πλέγμα. Παρατηρήστε ότι στο αντίστροφο πλέγμα οι αποστάσεις μετρώνται σε μονάδες L^-1 (για αυτό λέγεται αντίστροφο!) και ότι το μήκος της θεμελιώδους κυψελίδας του αντιστρόφου πλέγματος επί το μήκος της θεμελιώδους κυψελίδας του ευθέως πλέγματος ισούται με 2π.

Στις τρεις διαστάσεις, το πιο συνηθισμένο σύνολο διανυσμάτων του αντιστρόφου πλέγματος είναι να πάρουμε διανύσματα κάθετα στα διανύσματα του ευθέως πλέγματος. Η καθετότητα εξασφαλίζεται με το εξωτερικό γινόμενο:

Η κυψελίδα Wigner-Seitz του αντιστρόφου πλέγματος λέγεται ζώνη Brillouin. Ο όγκος της ζώνης Brillouin ισούται με (2π)³ δια τον όγκο της θεμελιώδους κυψελίδας.

Η ενέργεια σαν συνάρτηση της δομής: το μοντέλο ισότροπου στερεού ή μοντέλο Jellium.

Σε ένα στερεό η πυκνότητα προκύπτει από την εξισορρόπηση μεταξύ ηλεκτρομαγνητισμού (που θέλει όσο γίνεται πιο πυκνές δομές) και κβαντομηχανικής (που θέλει όσο γίνεται πιο αραιές δομές).

Λόγω ηλεκτρομαγνητισμού, η ολική δυναμική ενέργεια ενός συστήματος Ν θετικών και Ν αρνητικών φορτίων q είναι αρνητική. Η απόδειξη είναι περίπλοκη (δείτε πχ το θέμα 2.1 στο βιβλίο του Οικονόμου) αλλά μπορούμε να σκεφτούμε απλά ότι είναι θέμα συνδυαστικής: ο αριθμός των ζευγών (q,-q) που έλκονται είναι μεγαλύτερος από τον αριθμό των ζευγών (q,q) και (-q,-q) που απωθούνται. Από διαστατική ανάλυση βρίσκει κανείς ότι η δυναμική ενέργεια του συστήματος θα είναι της μορφής -λq²/(4πε₀r_s), όπου λ θετικός αριθμός.

Αντίθετα με την δυναμική ενέργεια, η κινητική ενέργεια των ηλεκτρονίων είναι χαμηλότερη όσο πιο αραιό είναι το στερεό. Η κινητική ενέργεια ηλεκτρονίου ισούται με p²/(2m), και p² ~ (Δp)² ~ (ħ/(Δx))² από την αρχή της αβεβαιότητας. Και διαστατικά προκύπτει το ίδιο αποτέλεσμα. H κινητική ενέργεια είναι λοιπόν της μορφής μ ħ²/(mr_s²), όπου μ θετικός αριθμός.

Η ολική ενέργεια σαν συνάρτηση της παραμέτρου r_s' τείνει στο άπειρο για μικρό r_s' και στο μηδέν για μεγάλο r_s'. Έχει ένα μοναδικό ελάχιστο όταν r_s'=r_s=2α/γ με τιμή U_min=α/r_s². H τιμή αυτή σχετίζεται με την ενέργεια συνοχής του στερεού και τα έργα ιονισμού του ατόμου με την σχέση U_σ=ζα/r_s²-Σ Ε_i. U_σ και Ε_i είναι οι απόλυτες τιμές της ενέργειας συνοχής και του i-οστού έργου ιονισμού. Το άθροισμα στο Σ πάει από i=1 έως i=ζ.

Απόκριση του στερεού σε πίεση

To μέτρο ελαστικότητας, Β, δείχνει πόσο θα αλλάξει ο όγκος ενός υλικού όταν του ασκηθεί πίεση P, σύμφωνα με τον ορισμό P=-B ΔV/V. Από τον ορισμό της πίεσης, P=-dU/dV και την σχέση που βρήκαμε μεταξύ U και r_s', μπορούμε να καταλήξουμε μετά από πολλές πράξεις ότι Β=α/(6πr_s⁵).

Στερεό συμπιέζεται με πίεση P και η πυκνότητά του αλλάξει κατά x=Δρ/ρ. Μπορεί να δειχθεί ότι από τον ορισμό του Β ισχύει P=Bx και ότι από το μοντέλο Jellium P=3B((1+x)^5/3-(1+x)^4/3). Οι δυο σχέσεις συμπίπτουν για x<<1. Εδώ μπορείτε να δείτε την γραφική παράσταση του x σαν συνάρτηση του λόγου P/B και εδώ την ίδια γραφική παράσταση για μικρό x. Παρατηρήστε ότι η σχέση είναι γραμμική με κλίση ίση με 1 στην περιοχή των μικρών x όπου οι δυο παραπάνω τύποι συμπίπτουν. Παρατηρήστε ότι για να αλλάξει αισθητά η πυκνότητα ενός στερεού απαιτούνται πιέσεις τουλάχιστον της τάξης του 1/100 του B, δηλαδή δεκάδες χιλιάδες ατμόσφαιρες.

Άσκηση: υπολογίστε και με τους δυο τύπους την πυκνότητα του Fe (α) υπό πίεση 10⁵N/cm²=1 GPa και (β) στο κέντρο της γης (P=3.6Mbar). Θα δείτε ότι ακόμα και για την τεράστια πίεση (α) οι δυο τύποι πρακτικά συμπίπτουν. Όμως στην περίπτωση (β) ο γραμμικός τύπος δίνει λάθος αποτέλεσμα. Ένας τρόπος εύρεσης της ρίζας της εξίσωσης P=f(x) είναι με το Wolfram alpha, όπως στο παράδειγμα.

Κίνηση των ηλεκτρονίων

(Κεφ. 3) Η κυματοσυνάρτηση ηλεκτρονίων στο μοντέλο Jellium.

Υπολογισμός της κινητικής ενέργειας των ηλεκτρονίων: δείξαμε ότι K_e=a/r_s² και το a ισούται (περίπου) με 1.1ħ²/m. Η μέση κινητική ενέργεια ισούται με τα 3/5 της ενέργειας Fermi.

Η πυκνότητα καταστάσεων, ρ(Ε) ορίζεται ως εξής: ο αριθμός ενεργειακών καταστάσεων ηλεκτρονίων οι οποίες έχουν ενέργειες στο διάστημα [Ε, Ε+dΕ) ισούται με ρ(Ε)dE. Συνήθως είναι πιο εύκολο να υπολογιστεί ο αριθμός καταστάσεων με ενέργεια μικρότερη ή ίση του Ε, R(E) και να υπολογιστεί το ρ(Ε) παραγωγίζοντας: ρ(Ε)=R'(E).

Υπολογισμός της πυκνότητας καταστάσεων ηλεκτρονίων για το μοντέλο Jellium δίνει ρ(Ε) ανάλογο του Ε στην 1/2. Γενικά μπορεί να αποδείξει κανείς ότι σε ένα σύστημα όπου η ενέργεια μιας ηλεκτρονικής κατάστασης εξαρτάται μόνο από το μέτρο του κυματανύσματος, ισχύει ο γενικός τύπος για την πυκνότητα καταστάσεων: ρ(Ε)~E^((d/ν)-1) όπου d η διάσταση του χώρου και ν o εκθέτης του k στη σχέση Ε=f(k).

Η συνθήκη κανονικοποίησης: το ολοκλήρωμα της ρ(Ε) μέχρι την ενέργεια Fermi ισούται με N/2.

Εφαρμογές: (α) επανάληψη του υπολογισμού για το a με χρήση της πυκνότητας καταστάσεων. (β )Υπολογισμός της ενέργειας, κυματάριθμου, ταχύτητας και θερμοκρασίας Fermi στον Cu.

Πυκνότητες καταστάσεων πραγματικών υλικών: Na, Al, Si. Κορυφές στην πυκνότητα καταστάσεων οφείλονται σε ηλεκτρονιακές καταστάσεις που δεν έχουν ομοιόμορφη συγκέντρωση ηλεκτρονίων, όπως πχ καταστάσεις που οφείλονται σε δεσμούς μεταξύ τροχιακών p. Στους ημιαγωγούς και μονωτές δεν υπάρχουν καταστάσεις σε μια περιοχή ενεργειών πάνω από την ενέργεια Fermi: αυτό λέγεται ενεργειακό χάσμα.

Κίνηση των ιόντων

(κεφ. 4) Απουσία εξωτερικών πεδίων, τα ιόντα και ηλεκτρόνια κινούνται (α) λόγω θερμοκρασίας και (β) λόγω της κβαντικής τους φύσης. Το (α) είναι αμελητέο για τα ηλεκτρόνια, αφού η θερμική ενέργεια είναι της τάξης του kT ενώ οι ενέργειες των ηλεκτρονίων κοντά στην ενέργεια Φερμι είναι της τάξης του kT_F, και T_F/Τ είναι της τάξης του 1000. Όμοια, το (β) είναι αμελητέο για τα ιόντα, αφού το αντίστοιχο R_s για ιόντα θα προέκυπτε 100000 μικρότερο από την ακτίνα τους. Αντίθετα, η θερμική ταλάντωση δίνει πλάτη ταλάντωσης κάπου 10 φορές μικρότερα από το μέγεθος του ιόντος, επομένως είναι αρκετά σημαντική.

Συμπέρασμα: τα e κινούνται μόνο λόγω της κβαντικής τους φύσης, ενώ τα ιόντα μόνο λόγω θερμικών δονήσεων.

2o διαγώνισμα. Αποτελέσματα

(Κεφ. 4) Ιδιοταλαντώσεις σε στερεά. Κάθε κίνηση των ιόντων μπορεί να αναλυθεί σε επίπεδα αρμονικά κύματα. Έστω u=R(t)-R₀ η μετατόπιση ενός ιόντος από την θέση ισορροπίας, R₀. Σε ένα επίπεδο αρμονικό κύμα, η μετατόπιση ενός απειροστού τμήματος του υλικού το οποίο βρίσκεται στο σημείο r και στον χρόνο t δίνεται από την σχέση u=u₀exp(q.r-ωt). To ω=2π/Τ είναι η κυκλική συχνότητα. To q είναι το κυματάνυσμα με φορά αυτήν της διάδοσης του κύματος και μέτρο τον κυματάριθμο, q=2π/λ. To ω και το q συνδέονται με περίπλοκες σχέσεις που λέγονται σχέσεις διασποράς. Σε απλό κύμα, θα ισχύει ω=cq, όπου c η ταχύτητα διάδοσης του κύματος. Το u₀ είναι το μέγιστο πλάτος της ταλάντωσης. Για κάθε τιμή του q, υπάρχουν τρεις ανεξάρτητες κατευθύνσεις ταλάντωσης, μια παράλληλη στο q (διαμήκες κύμα, συμβολίζεται με l) και δυο κάθετες στο q (εγκάρσια κύματα, συμβολίζονται με t).

Διαισθητικά περιμένουμε ότι θα πρέπει να υπάρχει ένα ελάχιστο μήκος κύματος για τα παραπάνω κύματα, το οποίο θα είναι της τάξης της διατομικής απόστασης. Αυτό υπαγορεύει ότι θα υπάρχει μια μέγιστη τιμή του κυματάριθμου, η οποία θα είναι της τάξης του κυματάριθμου Fermi, k_F. O μέγιστος κυματάριθμος για τις ιδιοταλαντώσεις των στερεών λέγεται κυματάριθμος Debye και συμβολίζεται με q_D.

Για να υπολογίσουμε το q_D εργαζόμαστε ως εξής: θα πρέπει ο συνολικός αριθμός ιδιοταλαντώσεων (=3 επί τον αριθμό των διαφορετικών q, αφού για κάθε q έχω 1 l και 2 t κύματα) να ισούται με τον συνολικό αριθμό ανεξάρτητων κινήσεων που μπορούν να εκτελέσουν τα άτομα του στερεού (= 3N_i, για την ακρίβεια 3N_i-6). Με βάση αυτό, καταλήγουμε ότι q_D=(6π²n_i)^1/3.

Η συχνότητα, ω, συνδέεται με το κυματάνυσμα, k με περίπλοκες εκφράσεις που εξαρτώνται από την κρυσταλλική δομή και την χημική σύσταση του υλικού. Σε ομοιογενές υλικό υπάρχουν μόνο οι ακουστικές ταλαντώσεις όπου ω=c_lq για διαμήκη κύματα και ω=c_tq για εγκάρσια κύματα. Τα διαμήκη κύματα έχουν μεγαλύτερη ταχύτητα από τα εγκάρσια (δείτε πχ τον πίνακα). Το γεγονός αυτό χρησιμοποιείται στην σεισμολογία και στον υπολογισμό της πυκνότητας του υπεδάφους.

Με διαστατική ανάλυση βρίσκουμε ότι μια εκτίμηση της ταχύτητας του ήχου σε στερεό είναι η c₀=(B/ρ_M)^1/2. O τύπος αυτός συμφωνεί απόλυτα με τα πειράματα για υγρά, και δίνει σε στερεά μια λογική τιμή, συνήθως ανάμεσα στις ταχύτητες εγκάρσιων και διαμηκών κυμάτων. Οι τελευταίες δίνονται από τον ίδιο τύπο, αλλά αντικαθιστώντας το Β με το κατάλληλο μέτρο ελαστικότητας από την θεωρία ελαστικότητας. Έτσι η ταχύτητα των εγκαρσίων κυμάτων σχετίζεται με το μέτρο διάτμησης και αυτή των διαμηκών κυμάτων με το μέτρο κύματος.

Η πυκνότητα καταστάσεων φωνονίων προκύπτει ανάλογη της ενέργειας στο τετράγωνο. Μπορεί να υπολογιστεί είτε θεωρώντας διαφορετικές ταχύτητες c_l και c_t, είτε μια μέση ταχύτητα που ορίζεται από την σχέση 3/c³=1/c_l³+2/c_t³. Το να θεωρήσουμε ότι διαμήκη και εγκάρσια κύματα έχουν ίδια ταχύτητα, c, απλοποιεί πολύ τις πράξεις ενώ δίνει σωστό αποτέλεσμα για την πυκνότητα καταστάσεων. Η προσέγγιση αυτή λέγεται μοντέλο Debye, και δίνει για την πυκνότητα καταστάσεων το αποτέλεσμα φ(ε)=9N_iε²/ε_D³.

Οι υπόλοιπες παράμετροι του μοντέλου Debye: ορίζουμε ως το ελάχιστο μήκος κύματος που μπορεί να διαδοθεί στο στερεό το λ_D=2π/q_D. Η μέγιστη συχνότητα ταλάντωσης των ιόντων είναι ω_D=c q_D. Η μέγιστη ενέργεια φωνονίου είναι ε_D=ħω_D. Η θερμοκρασία Θ_D, στην οποία η θερμική ενέργεια k_BΘ_D ισούται με την ενέργεια Debye λέγεται θερμοκρασία Debye. Ξεκινώντας από την τάξη μεγέθους του λ_D που είναι 1 Å και της ταχύτητας του ήχου, c, που είναι 1000 m/s, είναι εύκολο να δειχθεί ότι η τάξη μεγέθους της ενέργειας Debye είναι 10 meV και της θερμοκρασίας Debye είναι 100 Κ. Επομένως, σε αντίθεση με τα ηλεκτρόνια (θυμηθείτε ότι Τ_F~100000K), τα ιόντα έχουν σημαντικότατη θερμική κίνηση. Σε θερμοκρασία δωματίου περιμένουμε να συμμετέχουν στην θερμική κίνηση όλα τα είδη των φωνονίων, αφού ακόμα και η μέγιστη ενέργεια, ε_D, είναι μικρότερη, ή έστω συγκρίσιμη, με την θερμική ενέργεια k_BΤ.

Σύμφωνα με την κβαντική αρχή της συμπληρωματικότητας, κάθε κβαντικό φαινόμενο εκφράζεται με σωματιδιακή ή κυματική συμπεριφορά. Το σωματίδιο που συνοδεύει τις ιοντικές ταλαντώσεις λέγεται φωνόνιο. Η ενέργεια ενός φωνονίου ισούται με ε=ħω. Η ενέργεια μιας ιδιοταλάντωσης που έχει n φωνόνια δίνεται από την (n+1/2)ħω=(n+1/2)ε.

Απόκριση στερεού σε αύξηση της θερμοκρασίας.

Η ολική ενέργεια μιας ηλεκτρονικής κατάστασης με ενέργεια Ε είναι 2n(E)E, όπου n(E) o αριθμός κατάληψης (αριθμός ηλεκτρονίων στην κατάσταση αυτή). Για Τ=0 n(E)=1 αν Ε<Ε_F και 0 αν E>E_F. Αντίστοιχα, η ολική ενέργεια μιας ιοντικής ιδιοταλάντωσης με ενέργεια ε είναι (n(ε)+1/2)ε, όπου n(ε) o αριθμός κατάληψης (αριθμός φωνονίων στην κατάσταση αυτή). Για Τ=0 είναι n(ε)=0.

Χρησιμοποιώντας τα παραπάνω, μπορούμε να γράψουμε τους τύπους για τον αριθμό και την μέση ενέργεια ηλεκτρονίων Ν=∫2n(E)ρ(Ε)dE, και U_e=∫2n(E)Eρ(Ε)dE όπου τα ολοκληρώματα είναι από -άπειρο έως +άπειρο. (υπενθυμίζεται ότι στο μοντέλλο Jellium ρ(Ε)=0 για Ε<0).

Για τα φωνόνια δεν υπάρχει αντίστοιχος τύπος για τον αριθμό τους, υπάρχει όμως διατήρηση του αριθμού των καταστάσεων: 3Ν_i=∫ φ(ε)dε. H ενέργεια θα είναι U_i=∫(n(ε)+1/2)εφ(ε)dε, όπου τα ολοκληρώματα είναι από -άπειρο έως +άπειρο. (υπενθυμίζεται ότι στο μοντέλλο Debye φ(ε)=0 για ε<0 και ε>ε_D).

Σε μη μηδενική θερμοκρασία, το μόνο που αλλάζει είναι οι αριθμοί κατάληψης, n, στους παραπάνω τύπους, οι οποίοι δίνονται από τις κατανομές Fermi-Dirac και Bose-Einstein. Τα φωνόνια είναι μποζόνια με χημικό δυναμικό μ=0. Δείτε (πληροφοριακά) το αρχείο.

(Κεφ 5) Η θερμοχωρητικότητα C_V ορίζεται ως η μερική παράγωγος της εσωτερικής ενέργειας, U, ως προς την θερμοκρασία υπό σταθερό όγκο. Η U ισούται με το άθροισμα της κινητικής ενέργειας των ηλεκτρονίων, U_e, της δυναμικής ενέργειας των ηλεκτρονίων Δ_e=-γ/r_s, της ολικής ενέργειας των ιόντων U_i=U_φ+U_φ0. Οι όροι Δ_e και U_φ0 δεν εξαρτώνται από την θερμοκρασία. Επομένως η θερμοχωρητικότητα έχει δυο όρους οι οποίοι είναι οι παράγωγοι των U_e και U_φ: C_V=C_Ve+C_Vφ. Θα δείξουμε ότι σε θερμοκρασίες της τάξης των 10 Κ και μεγαλύτερες, η θερμοχωρητικότητα λόγω ηλεκτρονίων είναι αμελητέα και μπορεί να παραληφθεί.

Σε ψηλές θερμοκρασίες (δηλαδή θερμοκρασίες κοντά στην θερμοκρασία Debye του υλικού και μεγαλύτερες), μπορούμε να προσεγγίσουμε το εκθετικό στην κατανομή Bose Einstein με το ανάπτυγμα e^x=1+x, οπότε βρίσκουμε U_φ=k_ΒΤ∫ φ(ε)dε= 3Ν_ik_ΒΤ επομένως C_V=3Ν_ik_Β, ανεξάρτητο της θερμοκρασίας και ανεξάρτητο από το υλικό. Ο τύπος αυτός μπορεί να γραφεί με την μορφή c=3R/A, όπου c η θερμοχωρητικότητα ανά μονάδα μάζας, R η σταθερά των αερίων (R=N_Ak_B) και Α το μέσο ατομικό βάρος των ατόμων του υλικού. Η έκφραση cA=σταθερά είναι ο νόμος Dulong-Petit. Τα πειράματα των Dulong-Petit τον 19ο αιώνα απέδειξαν ξεκάθαρα την ατομική υπόθεση του Dalton και ο σχετικός νόμος αποτέλεσε την κύρια μέθοδο προσδιορισμού ατομικών βαρών.

Σε χαμηλές θερμοκρασίες, θα διεγερθούν φωνόνια χαμηλής ενέργειας, επομένως μικρού κυματάριθμου (αφού ε=ħcq), άρα μεγάλου μήκους κύματος (αφού q=2π/λ). Σε μεγάλα μήκη κύματος, όλα τα υλικά φαίνονται ομοιογενή, άρα θα ισχύει το μοντέλο Debye, με φ(ε)~ε² για 0<ε<ε_D και φ(ε)=0 για τις άλλες τιμές του ε. Εύκολα δείχνει κανείς ότι στο μοντέλο Debye για χαμηλή θερμοκρασία (T<<Θ_D) θα είναι C_V=(12π⁴/5)(T/Θ_D)³ Ν_ik_Β.

H θερμοχωρητικότητα λόγω ηλεκτρονίων είναι πιο δύσκολο να υπολογιστεί αναλυτικά, καθώς πρέπει να υπολογιστεί και το χημικό δυναμικό, μ, των ηλεκτρονίων. Καθώς όμως για τα ηλεκτρόνια η θερμοκρασία είναι πάντα πολύ μικρότερη από την θερμοκρασία Fermi, μπορούμε να κάνουμε την προσέγγιση U_e=∫2n(E)Eρ(Ε)dE = 2 (Ε_F+k_ΒT)ρ(Ε_F)k_ΒT, οπότε C_Ve=4ρ(Ε_F)k_Β²T. O σωστός τύπος, αν δεν θεωρούσαμε σταθερή την ολοκληρωτέα συνάρτηση, είναι πολύ παρόμοιος, με μια μικρή διαφορά στον αριθμητικό παράγοντα: C_Ve=(2π²/3)ρ(Ε_F)k_Β²T.

Εύκολα δείχνει κανείς ότι η θερμοχωρητικότητα λόγω ηλεκτρονίων είναι μικρότερη από την θερμοχωρητικότητα λόγω φωνονίων σε όλες τις θερμοκρασίες πάνω από λίγους βαθμούς K. Δείτε πχ μια απόδειξη στην σελ. 124 του βιβλίου του Οικονόμου.

3o διαγώνισμα.

Πέρα από την προσέγγιση του ομοιογενούς στερεού

Σε πραγματικά υλικά υπάρχουν εν γένει έξι διαφορετικά είδη φωνονίων, τα οποία χαρακτηρίζονται ως TA, LA, TO και LO ανάλογα με την πόλωση (Longitudal/transverse) και την συμεριφορά της συχνότητας για μικρό q (Αcoustic όταν το ω είναι ανάλογο του q και Οptical όταν το ω είναι σταθερό). Σε κάποια υλικά οι δυο εγκάρσιοι τρόποι έχουν διαφορετικές συχνότητες, οπότε θα υπάρχουν δύο Α και ένας L τρόποι οπτικών ταλαντώσεων και δύο Α και ένας L τρόποι ακουστικών ταλαντώσεων- σύνολο έξι. Δείτε πχ εδώ. Λόγω συμμετριών του υλικού, κάποιοι τρόποι ταλάντωσης μπορεί να έχουν ίδια συχνότητα. Πχ σε ένα ομοιογενές υλικό είδαμε ότι οι δυο εγκάρσιοι τρόποι έχουν ίδια συχνότητα, ενώ σε ένα ομοιογενές και ισότροπο υγρό όλοι οι τρόποι ταλάντωσης έχουν ίδια συχνότητα.

Το μοντέλο Einstein είναι το άλλο άκρο από το μοντέλο Debye: αντί να θεωρούμε το στερεό ως ένα ομοιογενές μέσο στο οποίο διαδίδονται ακουστικά κύματα, το θεωρούμε μια συλλογή ανεξάρτητων ταλαντωτών οι οποίοι δεν επηρεάζονται ο ένας από τον άλλο. Επομένως όλοι οι ταλαντωτές έχουν την ίδια συχνότητα, ω_E. Η πυκνοτητα καταστάσεων επομένως θα είναι μια συνάρτηση δέλτα, και συγκεκριμένα φ(ε)=3Ν_iδ(ε-ħω_E). Στο μοντέλο Einstein ο υπολογισμός της θερμοχωρητικότητας είναι πολύ απλός, και δίνει το σωστό αποτέλεσμα για ψηλές θερμοκρασίες. Ιστορικά, ο Einstein ήταν ο πρώτος που έδωσε μια αυστηρή θεωρητική βάση στον εμπειρικό νόμο των Dulong-Petit και επιπλέον έδωσε ένα μοντέλο που εξηγούσε την πτώση της θερμοχωρητικότητας των στερεών σε χαμηλές θερμοκρασίες. Το μοντέλο βέβαια δεν είναι τέλειο, καθώς δεν δίνει όμως σωστή εξάρτηση από την θερμοκρασία σε χαμηλές θερμοκρασίες. Το μοντέλο Debye περιγράφει τέλεια τα περισσότερα υλικά σε χαμηλές θερμοκρασίες αφού για μικρά q όλα τα υλικά μοιάζουν ομοιογενή. Όντως τα πειράματα δείχνουν ότι για μικρό T, είναι C_V=βΤ³+γΤ, με το γ να είναι μηδέν αν το υλικό δεν είναι μέταλλο. Δείτε ένα παράδειγμα στην εικόνα 6 αυτού του άρθρου.

Κίνηση ιόντων σε μονοδιάστατο νανοκαλώδιο

Έχουμε δείξει ήδη ότι οι ταλαντωτικές κινήσεις των ιόντων λόγω θερμικής κίνησης έχουν πλάτη της τάξης των 0.1 Å, δηλαδή οι διατομικές αποστάσεις (της τάξης των 2-3 Å) μεταβάλλονται ελάχιστα λόγω της κίνησης. Άρα μπορούμε να θεωρήσουμε ότι η ενέργεια σαν συνάρτηση της απόστασης γειτονικών ατόμων δίνεται από τους πρώτους όρους αναπτύγματος Taylor: U=U₀+½κ(d'-d)². O γραμμικός όρος απουσιάζει αφού η U έχει ελάχιστο για d'=d και άρα U'(d)=0. Επομένως για την μελέτη θερμικής κίνησης μπορούμε να θεωρούμε ότι το υλικό αποτελείται από σημειακές μάζες συνδεμένες με ελατήρια.

Στη μια διάσταση, το σύστημα λύνεται σχετικά εύκολα (βλ. Οικονόμου, κεφ. 1 ή Kittel, κεφ. 4, και βρίσκουμε σχέση διασποράς ω=ω_m|sin(qa/2)|, όπου a η απόσταση γειτονικών ατόμων και ω_m²=4κ/m_i. H σχέση αυτή μοιάζει με την σχέση του ομοιογενούς υλικού (ω=cq) για μικρά q, και δίνει c²=B/ρ όπου ρ=m_i/α είναι η γραμμική πυκνότητα και B=κα το μέτρο ελαστικότητας του υλικού (Β=-F ΔL/L). Για μεγάλα q, η σχέση δίνει οπτικά φωνόνια με σχέση διασποράς όμοια με αυτήν σωματιδίων με ενεργό μάζα m^*=-m_iħω_m/(κα²).

H πυκνότητα καταστάσεων φωνονίων είναι αντιστρόφως ανάλογη του (ω_m²-ω²)^½. Είναι μηδέν για ω<0, σταθερή για μικρό ω, απειρίζεται για ω κοντά στο ω_m και είναι μηδέν για ω>ω_m. Για σύγκριση, η πυκνότητα καταστάσεων στο μοντέλο Debye είναι μηδέν για ω<0, σταθερή για 0<<ω<ω_mπ/2 και μηδέν για μεγαλύτερα ω. Το μοντέλο Debye είναι σωστό στην περιοχή χαμηλών ενεργειών, όπου το υλικό φαίνεται ομοιογενές.

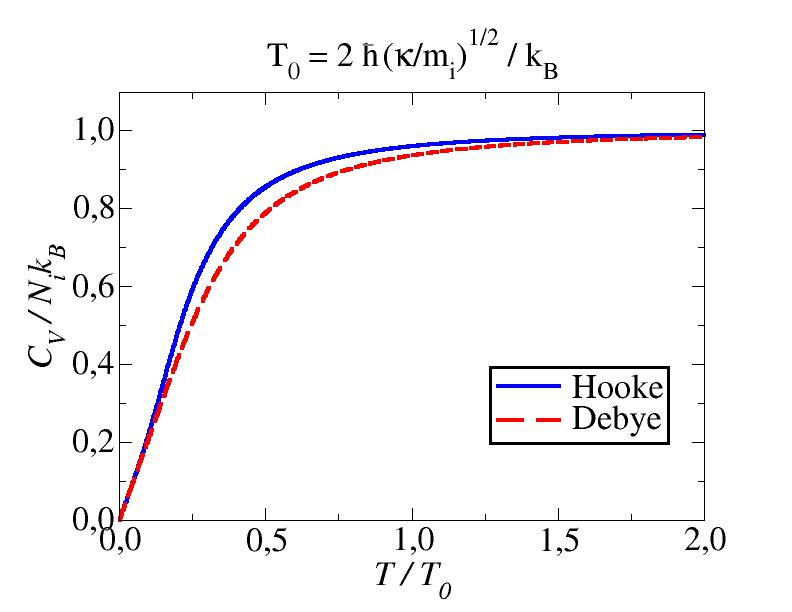
Παρότι το μοντέλο Debye δίνει πολύ διαφορετική πυκνότητα καταστάσεων από το πιο ρεαλιστικό μοντέλο των μαζών με ελατήρια, η θερμοχωρητικότητα δεν διαφέρει πολύ στα δυο μοντέλα. Ο λόγος είναι ότι η θερμοχωρητικότητα είναι ομαλή συνάρτηση της θερμοκρασίας (εφόσον δεν υπάρχει αλλαγή φάσης) και η εξάρτησή της απο την θερμοκρασία είναι: (α) σε ψηλές θερμοκρασίες ισούται με Ιk_B, όπου Ι το ολοκλήρωμα της πυκνότητας καταστάσεων (3Ν_i σε 3D , ή Ν_i σε 1D) και (β) σε χαμηλές θερμοκρασίες είναι ανάλογη του Τ^a+1 όταν η πυκνότητα καταστάσεων είναι ανάλογη της ενέργειας στην a. Στο μοντέλο Debye, η πυκνότητα καταστάσεων συμπίπτει με την πραγματική σε χαμηλές ενέργειες και έχει το σωστό ολοκλήρωμα, οπότε η θερμοχωρητικότητα βγαίνει σωστή και σε χαμηλές και σε ψηλές θερμοκρασίες. Για του λόγου το αληθές, η παρακάτω εικόνα συγκρίνει την θερμοχωρητικότητα του νανοκαλωδίου στην προσέγγιση μαζών με ελατήρια (Hooke) και στο μοντέλο Debye. Ο υπολογισμός έγινε χρησιμοποιώντας τους γνωστούς τύπους που δίνουν την θερμική ενέργεια U_φ από την πυκνότητας καταστάσεων και την κατανομής Bose-Einstein.

Κίνηση ηλεκτρονίων σε μονοδιάστατο νανοκαλώδιο

Θα μελετήσουμε την κίνηση των ηλεκτρονίων στα πλαίσια της θεωρίας LCAO (Linear Combination of Atomic Orbitals), η οποία είναι γνωστή και ως TB (Tight Binding) (βλ. Κεφ. 8.1 του Οικονόμου και κεφ 12 (παρ. 1.1) από "Κβαντομηχανική I" του Σ. Τραχανά). Στη μέθοδο αυτή η κυματοσυνάρτηση του ηλεκτρονίου γράφεται ως γραμμικός συνδυασμός ατομικών τροχιακών. Σε αντίθεση με την θεωρία του ομοιογενούς στερεού, η οποία είναι θεωρία πρώτων αρχών (τα αποτελέσματα περιέχουν μόνο παγκόσμιες σταθερές και σταθερές των ατόμων), η LCAO είναι ημιεμπειρική θεωρία. Βασίζεται στην κβαντομηχανική, αλλά εισάγει αρκετές παραμέτρους (το ε και το V₂ στην πιο απλή εκδοχή της) οι οποίες είναι αδύνατον να προσδιοριστούν από τη θεωρία ή το πείραμα, και ο ερευνητής τους δίνει τιμές ανάλογα με το πρόβλημα που έχει να λύσει, μέσα σε κάποια λογικά όρια. Η LCAO είναι μια θεωρία που δίνει πολύ ρεαλιστικά αποτελέσματα για τις ιδιότητες των υλικών, και είναι σήμερα μια από τις πιο δημοφιλείς μεθόδους στην μελέτη της ηλεκτρονικής δομής. Οι παράμετροι της LCAO ορίζονται από τις παρακάτω σχέσεις:

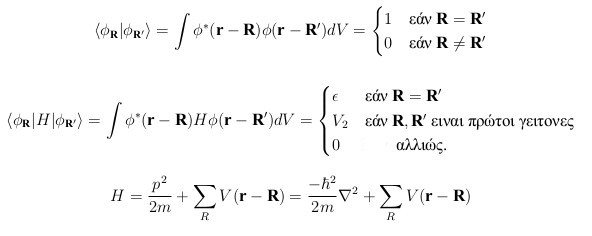
Η εφαρμογή της LCAO συνίσταται στα εξής βήματα:

1. Γράφουμε την κυματοσυνάρτηση ως γραμμικό συνδυασμό κατάλληλων ατομικών τροχιακών.
2. Κανονικοποιούμε στην μονάδα το ολοκλήρωμα της |ψ|².
3. Εφαρμόζουμε το θεώρημα Bloch αν είναι περιοδική δομή.
4. Αντικαθιστούμε την ψ στην εξίσωση Schrodinger, Ηψ=Εψ.
5. Πολλαπλασιάζουμε από αριστερά με φ^*(r) και ολοκληρώνουμε, ώστε να εμφανιστούν τα στοιχεία της παραπάνω εικόνας.
6. Επαναλαμβάνουμε το προηγούμενο βήμα αν υπάρχουν πάνω από ένα ατομικό τροχιακό στη βάση μας (πχ δυο είδη ατόμων, δυο τροχιακά ανά άτομο κλπ).
7. Λύνουμε την εξίσωση που προκύπτει, και βρίσκουμε την ενέργεια Ε. Αν έχω πολλά είδη ατομικών τροχιακών, θα προκύψει ομογενές σύστημα γραμμικών εξισώσεων, οπότε η Ε βρίσκεται θέτοντας την ορίζουσα ίση με μηδέν.

Αν εφαρμόσουμε την παραπάνω διαδικασία σε διατομικό μόριο με ίδια άτομα (πχ το H₂), θα βρούμε ότι στο μόριο υπάρχουν δυο στάθμες με ενέργειες ε+V₂ και ε-V₂. Για s τροχιακά το V₂ είναι αρνητικό, άρα η πρώτη κατάσταση έχει χαμηλότερη ενέργεια.

Η κυματοσυνάρτηση ηλεκτρονίου σε διατομικό μόριο είναι είτε δεσμική (άθροισμα των ατομικών κυματοσυναρτήσεων, χαμηλότερη ενέργεια από τις ατομικές στάθμες) είτε αντιδεσμική (διαφορά των ατομικών κυματοσυναρτήσεων, ψηλότερη ενέργεια από τις ατομικές στάθμες).

Η κυματοσυνάρτηση και η ενέργεια ηλεκτρονίου σε νανοκαλώδιο εξαρτώνται από τον πραγματικό κβαντικό αριθμό k με διαστάσεις κυματάριθμου, σύμφωνα με την σχέση ψ=Σ_n exp(inka) φ(x-na) και Ε=ε + 2V₂cos(ka).

Ανακοίνωση: Στις 19/12 θα κάνουμε μόνο διαγώνισμα την πρώτη ώρα και δεν θα κάνουμε μάθημα την Δεύτερη ώρα. Σε αναπλήρωση, θα προστεθεί ένα δίωρο την πρώτη εβδομάδα μετά τις γιορτές, με πιθανότερη ώρα 4-6 την Πέμπτη 9/1 (θα βγει κι άλλη ανακοίνωση για επιβεβαίωση).

Η παράμετρος V₂ δείχνει την αλληλεπίδραση μεταξύ τροχιακών γειτονικών ατόμων. Εύκολα αποδεικνύεται (βλ. "Κβαντομηχανική I" του Σ. Τραχανά σελ 529) ότι η παράμετρος V₂ είναι αρνητικός αριθμός αν οι ατομικές κυματοσυναρτήσεις είναι θετικές στην περιοχή όπου υπάρχει αλληλοεπικάλυψη. Επομένως όταν τα ατομικά τροχιακά είναι τύπου s, το V₂ είναι αρνητικός αριθμός. Εύκολα βρίσκεται διαστατικά ότι V₂=η ħ²/(md²), όπου m η μάζα του ηλεκτρονίου, d η απόσταση μεταξύ γειτονικών ατόμων και η είναι αδιάστατη παράμετρος. Το η εξαρτάται από το είδος των τροχιακών. Το πρόσημό του είναι θετικό αν τα δυο ατομικά τροχιακά έχουν ίδιο πρόσημο, και αρνητικό αν έχουν διαφορετικό. Η απόλυτη τιμή του η είναι της τάξης του 1. Στο κεφ. 10.2 του Οικονόμου δίνονται χαρακτηριστικές τιμές του V₂ για διάφορες περιπτώσεις απλών τροχιακών (δεν χρειάζεται να τις θυμάστε).

H ενεργός μάζα, m_*, ορίζεται από την σχέση Ε=ħ²/(m_*d²) η οποία ισχύει πάντα για μικρό k, καθώς σε αυτή την περιοχή όλα τα υλικά μοιάζουν ομοιογενή. Στο νανοκαλώδιο βρίσκουμε ότι η ενεργός μάζα είναι αντιστρόφως ανάλογη του V₂. Επομένως όσο πιο πυκνό το στερεό και πιο ισχυρή η αλληλεπίδραση γειτονικών ατόμων, τόσο πιο ελαφρύ φαίνεται το ηλεκτρόνιο. Αντίθετα, σε πολύ μικρή αλληλεπίδραση η ενεργός μάζα γίνεται τεράστια, το οποίο σημαίνει ότι το ηλεκτρόνιο κινείται με δυσκολία μέσα στο υλικό.

Η πυκνότητα καταστάσεων στο νανοκαλώδιο προκύπτει να απειρίζεται στα όρια της ζώνης. Ο κυματάριθμος Fermi ισούται με π/(2α) για ζ=1 (μισογεμάτη ζώνη) ή π/α για ζ=2 (γεμάτη ζώνη). Για σύγκριση, στο μοντέλο Jellium η πυκνότητα καταστάσεων είναι αντιστρόφως ανάλογη της τετραγωνικής ρίζας του Ε, άρα κι εκεί έχουμε απειρισμό στην ελάχιστη τιμή της ενέργειας. Μέχρι περίπου το μέσο της ζώνης, οι δυο πυκνότητες δεν διαφέρουν πολύ, αλλά από εκεί και πέρα υπάρχει τεράστια ποιοτική διαφορά. Eδώ μπορείτε να δείτε την σύγκριση των δυο πυκνοτήτων καταστάσεων. Οι άξονες έχουν τις ποσότητες x=(E-E_min)/(E_F-E_min) και y=ρ(Ε)(E_F-E_min)/Ν.

Τα παραπάνω αποτελέσματα γενικεύονται εύκολα και για στερεό τριών διαστάσεων σε απλό πλέγμα Bravais (δηλαδή μονοατομική βάση) με ένα τροχιακό ανά άτομο. Το αποτέλεσμα για την ενέργεια είναι Ε=ε+ΣV₂exp(ik.R). με το άθροισμα να είναι σε όλους τους πρώτους γείτονες του σημείου 0. Στην περίπτωση που έχουμε μόνο s τροχιακά, το V₂ δεν εξαρτάται από τον σχετικό προσανατολισμό τους, και καταλήγουμε ότι η ζώνη έχει κέντρο ε, ελάχιστο ε+zV₂ και μέγιστο ε-zV₂, όπου z είναι ο αριθμός σύνταξης (αριθμός πρώτων γειτόνων ενός ατόμου). Το εύρος της ζώνης είναι 2zV₂, και γίνεται μεγαλύτερο όσο περισσότεροι είναι οι γείτονες και όσο πιο ισχυρή η αλληλεπίδραση των τροχιακών τους. Όπως και στην ενεργό μάζα, όσο πιο πυκνό το στερεό και πιο έντονες οι αλληλεπιδράσεις, τόσο πιο ευνοϊκές είναι οι συνθήκες για την κίνηση των ηλεκτρονίων! Η εξήγηση είναι η κυματική φύση του ηλεκτρονίου.

Έκτακτο Μάθημα Ασκήσεων: Παρασκευή 13 Δεκεμβρίου, 4-6μμ, Αίθουσα Φ1.

Γενικεύοντας την παραπάνω συζήτηση, μπορούμε να φανταστούμε ότι σε ένα πραγματικό υλικό με πολλά είδη ατόμων και πολλά είδη τροχιακών, το κάθε είδος τροχιακού θα δημιουργήσει στο στερεό μια ζώνη γύρω από την ενέργειά του με εύρος 2zV₂. Στην περίπτωση που οι παράμετροι ε δυο τροχιακών είναι κοντινές, τότε οι ζώνες που θα δημιουργήσουν αυτά τα τροχιακά δεν είναι ανεξάρτητες αλλά εξαρτώνται και από παραμέτρους αλληλεπίδρασης μεταξύ τροχιακών. Αυτό οφείλεται στο ότι το ηλεκτρόνιο δεν θα περιοριστεί στο ένα ή στο άλλο τροχιακό, αλλά θα κινείται και στα δυο. Σε αυτή την περίπτωση, η ζώνη θα δημιουργηθεί γύρω από το υβριδικό τροχιακό (αν πρόκειται για τροχιακά ίδιου ατόμου) ή το μοριακό τροχιακό (αν πρόκειται για τροχιακά διαφορετικών ατόμων). Και στις δυο περιπτώσεις, το υβριδικό ή το μοριακό τροχιακό είναι γραμμικός συνδυασμός ατομικών τροχιακών.

Με βάση την παραπάνω θεωρία, καθοριστικό ρόλο για την ηλεκτρονική δομή του υλικού παίζει ο μέσος αριθμός ηλεκτρονίων σθένους ανά τροχιακό, δηλαδή το άθροισμα των ζ των ατόμων δια το άθροισμα των διαθέσιμων τροχιακών. Προφανώς ο αριθμός αυτός παίρνει τιμές μεταξύ 0 και 2. Αν είναι μικρότερος από 1 τότε κάποια ζώνη θα είναι μισογεμάτη, επομένως το υλικό είναι σίγουρα αγωγός. Αν είναι μεταξύ 1 και 2 τότε αν υπάρχει χάσμα μεταξύ της γεμάτης ζώνης και της επόμενης το υλικό είναι μονωτής ή ημιαγωγός ενώ αν δεν υπάρχει χάσμα το υλικό είναι αγωγός. Για ένα ηλεκτρόνιο ανά τροχιακό (όπως συμβαίνει στα υλικά δομής διαμαντιού, C, Si, Ge, Sn), το μέγεθος του χάσματος πέφτει καθώς μεγαλώνει η ακτίνα του ατόμου. Έτσι, τα υλικά αυτά ενώ έχουν ακριβώς ίδια ηλεκτρονική δομή έχουν πολύ διαφορετικές ηλεκτρικές ιδιότητες: Το διαμάντι είναι μονωτής, τα Si και Ge είναι ημιαγωγοί και ο Sn είναι μέταλλο. Η διαφορά μονωτών/ημιαγωγών έγκειται στο μέγεθος του χάσματος: συνήθως ημιαγωγοί θεωρούνται τα υλικά με χάσμα μικρότερο από 3 eV. Μπορείτε να δείτε μια σχηματική περιγραφή των ζωνών τυπικού ημιαγωγού σε σχέση με τα ατομικά τροχιακά στην εικόνα 12.1 του Οικονόμου.

Άσκηση: υπολογισμός της μέσης κινητικής ενέργειας σε νανοκαλώδιο με ζ=1 και για θερμοκρασία Τ=0, πρώτα με τη μέθοδο LCAO και μετά με την προσέγγιση ομοιογενούς στερεού. Καθώς τα δυο μοντέλα έχουν διαφορετική ελάχιστη ενέργεια, αλλά και ενέργεια Φέρμι, συγκρίνουμε τον λόγο (K_e-E_min)/(E_F-E_min). Βρίσκουμε ότι αυτός έχει τιμή 1/3 στο μοντέλο Jellium και 1-2/π στο LCAO. Παρότι τα δυο μοντέλα διαφέρουν πολύ σε ψηλές ενέργειες, δεν έχουν μεγάλη διαφορά σε χαμηλές ενέργειες και αυτό φαίνεται και σε αυτόν τον υπολογισμό που δίνει 0.33 για το ένα μοντέλο και 0.36 για το άλλο.

Ανακοίνωση: Στις 19/12 θα γράψουμε διαγώνισμα την πρώτη ώρα (11-12) και δεν θα κάνουμε μάθημα την δεύτερη ώρα. Μετά τις διακοπές θα γίνουν τα εξής μαθήματα, στα οποία θα καλυφθεί ύλη από τα κεφ. 6 και 7 του βιβλίου του Οικονόμου (ηλεκτρικές-μαγνητικές ιδιότητες):

1. Τρίτη, 7/1: 11-1 θεωρία Με νεώτερη απόφαση της Σχολής, η 7/1 είναι αργία και δεν γίνονται μαθήματα.
2. Πέμπτη, 9/1: 11-1 θεωρία.
3. Πέμπτη, 9/1: 4-6 θεωρία (αίθουσα 2).
4. Τρίτη, 14/1: 11-12 θεωρία, 12-1 ασκήσεις.
5. Πέμπτη, 16/1: 11-12 διαγώνισμα.

4o διαγώνισμα.