Η έννοια της νανοτεχνολογίας
Από την ομιλία του Richard Feynmann, "There's Plenty of Room at the Bottom", το 1959:- Εκτιμήστε πόση σμύκρινση απαιτείται για να γραψουμε μια εγκυκλοπαίδεια στο κεφάλι μιας καρφίτσας. Σε αυτή τη σμίκρυνση, βρείτε πόσα άτομα θα χρειαστούν για να απεικονιστεί η μικρότερη κουκίδα πλάτους 0.2 mm.
- Υποθέστε τώρα ότι, αντί να χρησιμοποιήσουμε αυτά τα άτομα για να απεικονίσουμε μια κουκίδα, τα χρησημοποιούμε για να εγγράψουμε 1 bit πληροφορίας. Βρείτε πόσα άτομα απαιτούνται για να εγγράψουμε το κείμενο από όλα τα βιβλία του κόσμου. Δείξτε ότι χρειάζεται υλικό όσο περίπου ένας κόκος σκόνης. Υποθέστε ότι υπάρχουν περίπου 107 βιβλία. Πώς θα μπορούσαμε να εκτιμήσουμε τον αριθμό αυτό;
- Γιατί η σημερινή τεχνολογία, παρότι έχει προ πολλού ξεπεράσει το επίπεδο (1), απέχει πάρα πολύ από το επίπεδο (2);
Οι βασικές φυσικές ιδιότητες που χαρακτηρίζουν τα νανοϋλικά
- Πολλά άτομα σε επιφάνειες σε σχέση με τα εσωτερικά άτομα.
- Κβαντισμένες στάθμες, με χάσματα συγκρίσιμα με τις ενέργειες οπτικών φωτονίων.
- Η ενέργεια που απαιτείται για να προστεθεί ή να αφαιρεθεί ένα ηλεκτρόνιο είναι πολύ μεγαλύτερη της θερμικής ενέργειας kT.
Για να καταλάβετε τη θεμελιώση σχέση μεταξύ επιφανειών και νανοϋλικών, υπολογίστε το λόγο του αριθμού των εσωτερικών ατόμων προς τον αριθμό των ατόμων της επιφάνειας σε μια απλή κυβική διάταξη ατόμων, όταν η ακμή του κύβου είναι (α) 1 cm και (β) 1 nm.
Θεωρήστε ένα καλώδιο μήκους L, και ένα ηλεκτρόνιο που κινείται ελεύθερα κατα μήκος του, αλλά δεν μπορεί να κινηθεί εκτός του καλωδίου. Λύστε την εξίσωση Schrodinger στο σύστημα και προσδιορίστε τις ιδιοενέργειες και τις ιδοσυναρτήσεις του ηλεκτρονίου. Δείτε πχ στο βιβλίο του Σ. Τραχανά, Κβαντομηχανική Ι, Ηράκλειο 2005, κεφ. 5, σελ. 217.
Θεωρήστε τώρα ότι έχουμε Ν ηλεκτρόνια στο καλωδιο. Ο αριθμός Ν μπορεί να εκτιμηθεί θεωρώντας ότι στην ύλη σε κάθε άτομο (διαμέτρου 0.2-0.3 nm) αντιστοιχούν 1-3 ηλεκτρόνια σθένους, άρα N/L είναι περίπου 10 nm-1 Εκτιμήστε τις ενέργεις που σχετίζονται με πρόσθεση ή αφαίρεση ενός ηλεκτρονίου από το σύστημα, όταν το μήκος του καλωδίου είναι 1 nm ή 1 μm ή 1 cm. Παρατηρήστε ότι μόνο στην περίπτωση των νανοϋλικών έχω μετρήσιμες ενέργειες, οι οποίες μάλιστα είναι κοντά στις ενέργειες οπτικών φωτονίων. Δηλαδή τα νανοϋλικά απορροφούν ενέργεια στο ορατό. Εφαρμογές στο νανοτρανζίστορ (το link ανοίγει μόνο από το Π.Κ.).
Δείξτε ότι οι ενέργειες που βρήκατε είναι πολύ μεγαλύτερες από τη θερμική ενέργεια (kT). Τι σημαίνει αυτό; Το φαινόμενο αυτό λέγεται κβαντική φραγή Coulomb. Μελετήστε το κλασσικό ανάλογο, που είναι η φόρτιση μεταλλικού σώματος με το ελάχιστο φορτίο, e. Πάρτε για απλότητα μια σφαίρα ακτίνας R. Δείξτε ότι η ενέργεια φόρτισης γίνεται πολύ μεγαλύτερη του kT όταν το R πέσει στην περιοχή του nm.
Ατομική δομή επιφανειών στερεών
Οι βασικές φυσικές και χημικές διεργασίες που συμβαίνουν σε επιφάνειες, και η σχέση επιφανειών-νανοϋλικών. Εύρεση του ρυθμού πρόσκρουσης των μορίων του αέρα σε επιφάνεια με χρήση διαστατικής ανάλυσης.
Ο ρυθμός με τον οποίο συγκρούονται τα άτομα αερίου με μια επιφάνεια δίνεται από τον τύπο του Knudsen, Z=P/√(2πmkT), όπου P είναι η πίεση του αερίου, Τ η θερμοκρασία και m η μέση μάζα των μορίων του αερίου. Με βάση αυτόν τον τύπο, μπορούμε να δείξουμε ότι σε K.Σ μια επιφάνεια θα καλυφθεί πλήρως σε μερικά ns! Βρείτε πόση πρέπει να γίνει η πίεση ώστε να έχουμε καθαρές επιφάνειες για μερικές ώρες. Η επιστήμη επιφανειών, που απαιτεί καλά ορισμένες και καθαρές επιφάνειες, γεννήθηκε τη δεκαετία του '80, οπότε και κατασκευάστηκαν καλές συσκευές υπερυψηλού κενού (Ultra-High Vacuum, UHV).
Νέες έννοιες:
- 1 ML (monolayer) είναι η ποσότητα ατόμων (πχ αέρα) που απαιείται για να καλυφθούν πλήρως όλα τα άτομα μιας επιφάνειας.
- Θεμελιώδης κυψελίδα είναι το σχήμα που επαναλαμβανόμενο αυτούσιο παράγει όλη τη δομή.
- Τα a1 και a2 λέγονται διανύσματα βάσης, αν κάθε κυψελίδα της δομής απέχει από κάθε άλλη κατά R=n1a1+n1a2, όπου n1 και n2 ακέραιοι.
- Επιφανειακή συγκέντρωση, ns: αριθμός επιφανειακών ατόμων ανά μονάδα εμβαδού.
- Εμβαδόν ανά άτομο: το αντίστροφο της συγκέντρωσης.
- Πλήρωση, f: το ποσοστό του εμβαδού της επιφάνειας που καταλμβάνεται από άτομα, αν θεωρήσουμε ότι τα άτομα είναι σφαίρες με ακτίνα το μισό της μικρότερης διατομικής απόστασης.
Άσκηση (από τον Atkins): Αέριο ήλιο σε P=35 Pa και Τ=80 Κ βρίσκεται σε ισοροπία με επιφάνεια Cu(100). Υπολογίστε πόσες φορές το δευτερόλεπτο κατά μέσο όρο συγκρούονται άτομα He σε ένα άτομο της επιφάνειας. Ο Cu έχει δομή fcc με a=351 pm.
Εύρεση θεμελιωδών κυψελίδων, διανυσμάτων βάσης, συγκέντρωσης και πλήρωσης για τις επιφάνειες μέγιστης πλήρωσης, fcc(111) και hcp(001).
Η επιφανειακή ενέργεια είναι το μισό της ενέργεια που απαιτείται για να κόψουμε στα δυο ένα στερεό. Η επιφανειακή ενέργεια εξαρτάται από το εμβαδόν της δημιουργηθείσας επιφάνειας και από τον προσανατολισμό της. Επιφανειακή τάση είναι η επιφανειακή ενέργεια ανά μονάδα εμβαδού.
Το μοντέλο των ακόρεστων δεσμών εκφράζει την επιφανειακή ενέργεια ως NdbEdb, όπου Ndb ο αριθμός των ακόρεστων δεσμών και Edb η ενέργεια ανά ακόρεστο δεσμό. Αυτή μπορεί να θεωρηθεί ότι ισούται περίπου με Ec/z, όπου Ec είναι η ενέργεια συνοχής ανά άτομο και z είναι ο αριθμός πλησιέστερων γειτόνων στον τέλειο κρύσταλλο.
Παράδειγμα: σε κρύσταλλο δομής fcc είναι z=12, άρα Edb=Ec/12. Στην (111) υπάρχουν Ndb=12-9=3 ακόρεστοι δεσμοί και το εμβαδόν ανά άτομο είναι d2√3/2, όπου d η απόσταση γειτόνων. Άρα σ=√3/6 Ec/d2. Στην (100) Ndb=12-8=4 ακόρεστοι δεσμοί και το εμβαδόν ανά άτομο είναι d2, όπου d η απόσταση γειτόνων. Άρα σ=1/3 Ec/d2.
Σχήμα των νανοσωματιδίων και επιφανειακές τάσεις
Το σχήμα των νανοσωματιδίων καθορίζεται από δυο κυρίως παράγοντες: τη συμμετρία της κρυσταλλικής δομής και τις διαφορές στην επιφανειακή τάση από επιφάνεια σε επιφάνεια. Στα νανοσωμάτια που φτιάχνονται πάνω σε υπόστρωμα, όπως στους καταλύτες, παίζει ρόλο και η διεπιφανειακή τάση.
 Το νανοσωματίδιο πρέπει να έχει τις ίδιες συμμετρίες που έχει και το αντίστοιχο υλικό. Για παράδειγμα, σε ένα υλικό με κυβική κρυσταλλική δομή (fcc, bcc, sc, diamond, NaCl κτλ) ο κρύσταλλος φαίνεται πανομοιότυπος
αν περιστραφεί κατά 90o γύρω από τρεις άξονες,
οι οποίοι είναι κάθετοι μεταξύ τους. Αυτό σημαίνει ότι επιφάνειες που είναι κάθετες μεταξύ τους έχουν ίδια δομή, και επομένως και ίδια επιφανειακή ενέργεια. Αυτό πχ συμβαίνει με τις (100), (010) και (001) οι οποίες είναι όλες ισοδύναμες σε κρυστάλλους με κυβική συμμετρία. Αντίθετα, αν ο κρύσταλλος έχει εξαγωνική συμμετρία, όπως πχ η δομή hcp, οι έδρες (100) και (001) θα είναι εν γένει πολύ διαφορετικές. Υλικό με κυβική συμμετρία δεν μπορεί να φτιάχνει πυραμιδοειδή νανοσωμάτια, αφού
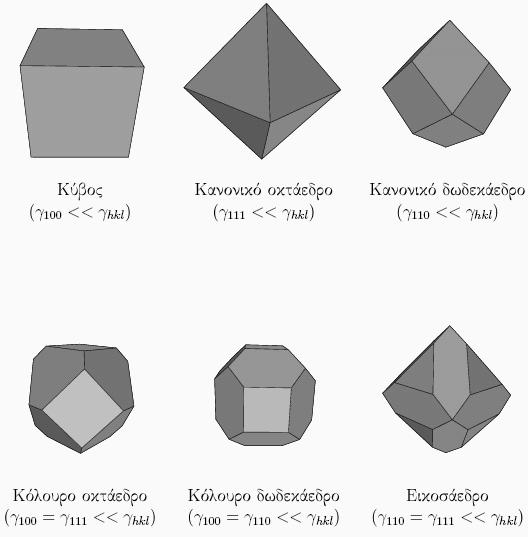
μια πυραμίδα δεν έχει τρεις κάθετους άξονες συμμετρίας, αλλά μόνο έναν. Αντίθετα, όλα τα παρακάτω σχήματα έχουν τις ίδιες συμμετρίες που έχει και ο κύβος, και άρα θα μπορούσαν να φτιαχτούν νανοσωμάτια τέτοιου σχήματος από κυβικής συμμετρίας υλικά:
Το νανοσωματίδιο πρέπει να έχει τις ίδιες συμμετρίες που έχει και το αντίστοιχο υλικό. Για παράδειγμα, σε ένα υλικό με κυβική κρυσταλλική δομή (fcc, bcc, sc, diamond, NaCl κτλ) ο κρύσταλλος φαίνεται πανομοιότυπος
αν περιστραφεί κατά 90o γύρω από τρεις άξονες,
οι οποίοι είναι κάθετοι μεταξύ τους. Αυτό σημαίνει ότι επιφάνειες που είναι κάθετες μεταξύ τους έχουν ίδια δομή, και επομένως και ίδια επιφανειακή ενέργεια. Αυτό πχ συμβαίνει με τις (100), (010) και (001) οι οποίες είναι όλες ισοδύναμες σε κρυστάλλους με κυβική συμμετρία. Αντίθετα, αν ο κρύσταλλος έχει εξαγωνική συμμετρία, όπως πχ η δομή hcp, οι έδρες (100) και (001) θα είναι εν γένει πολύ διαφορετικές. Υλικό με κυβική συμμετρία δεν μπορεί να φτιάχνει πυραμιδοειδή νανοσωμάτια, αφού
μια πυραμίδα δεν έχει τρεις κάθετους άξονες συμμετρίας, αλλά μόνο έναν. Αντίθετα, όλα τα παρακάτω σχήματα έχουν τις ίδιες συμμετρίες που έχει και ο κύβος, και άρα θα μπορούσαν να φτιαχτούν νανοσωμάτια τέτοιου σχήματος από κυβικής συμμετρίας υλικά:
Το σχήμα του νανοσωματιδίου είναι τέτοιο ώστε να ελαχιστοποιείται η επιφανειακή ενέργεια. Για δεδομένη ποσότητα του υλικού, το σύστημα θα επιλέξει το σχήμα εκείνο το οποίο ελαχιστοποιεί τη συνολική επιφανειακή ενέργεια. Η τελευταία ισούται με το άθροισμα όρων της μορφής γhklAhkl, όπου γhkl είναι η επιφανειακή τάση της επιφάνειας (hkl) και Ahkl το εμβαδόν της επιφάνειας αυτής στο νανοσωμάτιο. Αν μια έδρα έχει αρκετά χαμηλότερη ενέργεια από τις άλλες, τότε αυτή θα καθορίζει το σχήμα.
Παράδειγμα: Στο NaCl, υλικό με κυβική συμμετρία, βρίσκουμε ότι η (100) έχει επιφανειακή τάση ε/α2, όπου ε η ενέργεια ενός ακόρεστου δεσμού και α η πλεγματική σταθερά. Για τις (110) και (111) βρίσκουμε επιφανειακές τάσεις κατά 2√2 και 4√3 μεγαλύτερες, αντίστοιχα. Επομένως, με βάση το παραπάνω σχήμα, περιμένουμε το σχήμα των κρυστάλλων του ορυκτού αλατιού να είναι κυβικό, όπως και είναι. Παράδειγμα ΙΙ: Στο διαμάντι, επίσης υλικό με κυβική συμμετρία, βρίσκουμε ότι η (100) έχει ενέργεια 4ε/α2, όπου ε η ενέργεια ενός ακόρεστου δεσμού και α η πλεγματική σταθερά. Για την (110) βρίσκουμε 2√2ε/α2 και για την (111) βρίσκουμε (4/√4)ε/α2. Η (111) έχει πολύ χαμηλότερη ενέργεια, άρα με βάση το παραπάνω σχήμα το σχήμα των ακατέργαστων διαμαντιών, αλλά και των νανοσωματιδίων Si κλπ, θα πρέπει να είναι κανονικό οκτάεδρο. Και όντως είναι. Δείτε και εδώ.

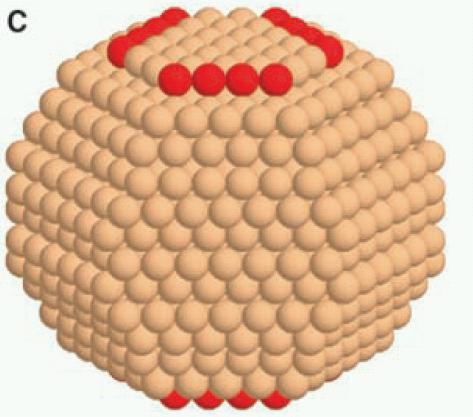 Γενικά, το σχήμα ελάχιστης ενέργειας θα περιέχει πολλών ειδών έδρες. Στην παραπάνω εικόνα φαίνονται σχήματα που περιέχουν μόνο ένα ή μόνο δυο είδη. Σε ένα νανοσωμάτιο Ru, για παράδειγμα,
όπως αυτό του διπλανού σχήματος,εμφανίζονται τουλάχιστον 4 διαφορετικές έδρες (οι 001, 100, 101, 201 -προσέξτε ότι άλλο η 001, άλλο η 100, καθώς το Ru έχει δομή hcp!). Iσχύει το
Θεώρημα Wulff:Το σχήμα ελάχιστης επιφανειακής ενέργειας είναι εκέινο για το οποίο dhkl/γhkl=σταθερό.
Γενικά, το σχήμα ελάχιστης ενέργειας θα περιέχει πολλών ειδών έδρες. Στην παραπάνω εικόνα φαίνονται σχήματα που περιέχουν μόνο ένα ή μόνο δυο είδη. Σε ένα νανοσωμάτιο Ru, για παράδειγμα,
όπως αυτό του διπλανού σχήματος,εμφανίζονται τουλάχιστον 4 διαφορετικές έδρες (οι 001, 100, 101, 201 -προσέξτε ότι άλλο η 001, άλλο η 100, καθώς το Ru έχει δομή hcp!). Iσχύει το
Θεώρημα Wulff:Το σχήμα ελάχιστης επιφανειακής ενέργειας είναι εκέινο για το οποίο dhkl/γhkl=σταθερό.
Στον παραπάνω τύπο, dhkl είναι η απόσταση του επιπέδου hkl από το κέντρο του νανοσωματιδίου, και γhkl η επιφανειακή τάση. Με εφαρμογή του θεωρήματος βρίσκουμε πχ ότι σε υλικό με κυβική συμμετρία και γ111 < γ110 < γhkl για όλα τα άλλα (hkl), το σχήμα είναι κανονικό οκάεδρο, εκτός εάν συμβεί να είναι γ111/γ110 > √2/√3.
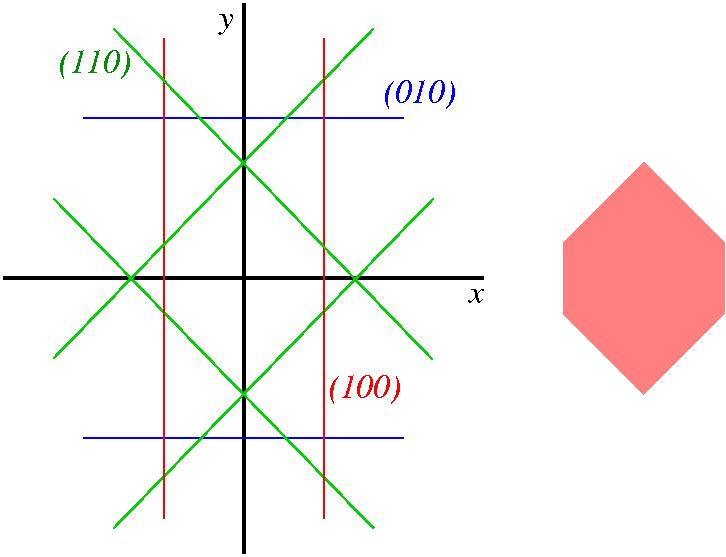 Εφαρμογή: σε κάποιο υλικό είναι γ100=γ110=γ-110=γ, γ010=2γ=γ001, και γhkl > 2γ για όλα τα άλλα επίπεδα. Βρείτε το σχήμα ελάχιστης ενέργειας. Λύση: Το παρακάτω σχήμα δείχνει την κάτοψη του νανοσωματιδίου. Τοποθετούμε το επίπεδο (100), το οποίο είναι παράλληλο με το επίπεδο yz σε απόσταση 1 από την αρχή. Τοποθετούμε συμμετρικά του το (-100) (κόκκινο). Τοποθετούμε τα επίπεδο (010) και (0-10), τα οποία είναι παράλληλο με το επίπεδο xz, σε απόσταση 2 από την αρχή, αφού γ010=2γ100 (μπλέ). Το επίπεδο (110) θα είναι παράλληλο με την ευθεία x+y=0 στο επίπεδο xy, και θα απέχει επίσης 1 από την αρχή (πράσινο). Το (-110) θα είναι παράλληλο με την ευθεία -x+y=0 στο επίπεδο xy, και θα απέχει επίσης 1 από την αρχή (πράσινο). Τέλος σχεδιάζω και τα συμμετρικά τους, (-1-10) και (1-10). Το σχήμα του νανοσωματιδίου θα περικλείεται από τα επίπεδα που σχεδιάσαμε, και θα είναι ένα πρίσμα με εξαγωνική βάση, η οποία φαίνεται δεξιά. Δεν χρειάζεται να ανησυχούμε για άλλες έδρες, αφού η συνθήκη
γhkl > 2γ υπαγορεύει ότι θα απέχουν πάνω από 2 από την αρχή και άρα δεν θα επηρεάζουν το σχήμα.
Εφαρμογή: σε κάποιο υλικό είναι γ100=γ110=γ-110=γ, γ010=2γ=γ001, και γhkl > 2γ για όλα τα άλλα επίπεδα. Βρείτε το σχήμα ελάχιστης ενέργειας. Λύση: Το παρακάτω σχήμα δείχνει την κάτοψη του νανοσωματιδίου. Τοποθετούμε το επίπεδο (100), το οποίο είναι παράλληλο με το επίπεδο yz σε απόσταση 1 από την αρχή. Τοποθετούμε συμμετρικά του το (-100) (κόκκινο). Τοποθετούμε τα επίπεδο (010) και (0-10), τα οποία είναι παράλληλο με το επίπεδο xz, σε απόσταση 2 από την αρχή, αφού γ010=2γ100 (μπλέ). Το επίπεδο (110) θα είναι παράλληλο με την ευθεία x+y=0 στο επίπεδο xy, και θα απέχει επίσης 1 από την αρχή (πράσινο). Το (-110) θα είναι παράλληλο με την ευθεία -x+y=0 στο επίπεδο xy, και θα απέχει επίσης 1 από την αρχή (πράσινο). Τέλος σχεδιάζω και τα συμμετρικά τους, (-1-10) και (1-10). Το σχήμα του νανοσωματιδίου θα περικλείεται από τα επίπεδα που σχεδιάσαμε, και θα είναι ένα πρίσμα με εξαγωνική βάση, η οποία φαίνεται δεξιά. Δεν χρειάζεται να ανησυχούμε για άλλες έδρες, αφού η συνθήκη
γhkl > 2γ υπαγορεύει ότι θα απέχουν πάνω από 2 από την αρχή και άρα δεν θα επηρεάζουν το σχήμα.
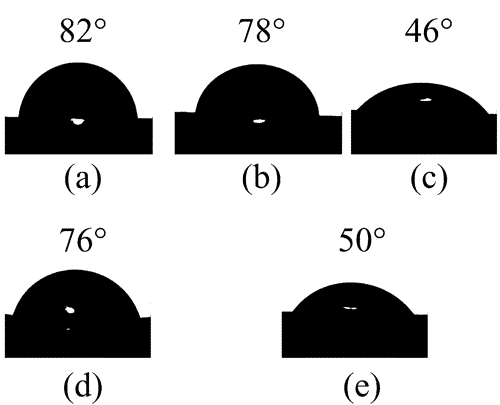 Στην περίπτωση που το υλικό δεν είναι σε ομοιγενές περιβάλλον, αλλά συγκρατείται πάνω σε μια επιφάνεια, το σχήμα του καθορίζεται από
το συνδυασμό των επιφανειακών τάσεων αλλά και της διεπιφανειακής τάσης μεταξύ του υλικού και της επιφανειας. Νανοσωμάτια που συγκρατούνται πάνω σε επιφάνειες θα προσπαθήσουν είτε να έχουν μεγάλο εμβαδόν της διεπιφάνειας, εαν συμβεί η διεπιφάνεια να έχει χαμηλότερη ενέργεια από την επιφάνεια του υποστρώματος. Στην αντίθετη περίπτωση το εμβαδόν της διεπιφάνειας θα είναι μικρό. Η συνάφεια μεταξύ του υλικού και του υποστρώματος αντικατοπτρίζεται στη γωνία επαφής (contact angle), θ. Στην περίπτωση μεγάλης συνάφειας, η γωνία επαφής είναι οξεία, ενώ στην περίπτωση μικρής συνάφειας είναι αμβλεία. Για παράδειγμα, η διπλανή εικόνα δείχνει διάφορες γωνίες επαφής για διεπιφάνεια μεταξύ μιας σταγόνας νερού και διαφόρων πολυμερικών υποστρωμάτων.
Στην περίπτωση που το υλικό δεν είναι σε ομοιγενές περιβάλλον, αλλά συγκρατείται πάνω σε μια επιφάνεια, το σχήμα του καθορίζεται από
το συνδυασμό των επιφανειακών τάσεων αλλά και της διεπιφανειακής τάσης μεταξύ του υλικού και της επιφανειας. Νανοσωμάτια που συγκρατούνται πάνω σε επιφάνειες θα προσπαθήσουν είτε να έχουν μεγάλο εμβαδόν της διεπιφάνειας, εαν συμβεί η διεπιφάνεια να έχει χαμηλότερη ενέργεια από την επιφάνεια του υποστρώματος. Στην αντίθετη περίπτωση το εμβαδόν της διεπιφάνειας θα είναι μικρό. Η συνάφεια μεταξύ του υλικού και του υποστρώματος αντικατοπτρίζεται στη γωνία επαφής (contact angle), θ. Στην περίπτωση μεγάλης συνάφειας, η γωνία επαφής είναι οξεία, ενώ στην περίπτωση μικρής συνάφειας είναι αμβλεία. Για παράδειγμα, η διπλανή εικόνα δείχνει διάφορες γωνίες επαφής για διεπιφάνεια μεταξύ μιας σταγόνας νερού και διαφόρων πολυμερικών υποστρωμάτων.
Η σχέση γωνίας επαφής και διεπιφανειακής τάσης δίνεται από τον τύπο του Young, γ2=γint+γ1cosθ, όπου γ2 είναι η επιφανειακή τάση του υποστρώματος, γ1 η επιφανειακή τάση του υλικού ή του νανοσωματιδίου, γint η διεπιφανειακή τάση και θ η γωνία επαφής. Οι επιφάνειες των υγρών ασκούν δύναμη παράλληλη προς αυτές με μέτρο F=γL, όπου γ είναι η επιφανειακή τάση και L το μήκος της επιφάνειας κάθετα στην κατεύθυνση του F. Η επιφανειακή τάση εκφράζει την απροθυμία των υγρών να αυξήσουν το εμβαδόν της επιφάνειάς τους.
'Ασκηση: Ρίχνουμε μια σταγόνα νερού σε επιφάνεια υδραργύρου και παρατηρούμε ότι η γωνία επαφής ήταν 33.3o. Η επιφανειακή τάση του νερού είναι 0.073 J/m2 και του υδραργύρου 0.436 J/m2. Βρείτε τη διεπιφανειακή τάση. 'Ασκηση: Βρείτε τι σχήμα θα πάρει μια σταγόνα βενζίνης πάνω σε επιφάνεια νερού. Η επιφανειακή τάση της βενζίνης και του νερού είναι 0.029 J/m2 και 0.073 J/m2, αντίστοιχα, και η διεπιφανειακή τους τάση είναι 0.035 J/m2. Καθώς η βενζίνη ανακατεύεται με το νερό, η επιφανειακή τάση του νερού μειώνεται στα 0.062 J/m2. Επαναλάβετε τον υπολογισμό.Προσρόφηση αερίων σε επιφάνειες στερεών
Περιγραφή επιφανειών με διανύσματα βάσης, ονοματολογία αναδομήσεων και υπερδομών (δηλαδή δομών που δημιουργούνται από προσρόφηση ατόμων ή μορίων): Έστω ότι τα διανύσματα της ιδανικής επιφάνειας είναι a1 και a2, και ότι τα διανύσματα της υπερδομής είναι A1 και A2. Συμβολισμός Wood: λέμε ότι έχουμε δομή (m x n)Rφ, αν ισχύει |Α1|=m|a1|, |Α2|=n|a2| και η γωνία μεταξύ a0 και as, όπως και η γωνία μεταξύ b0 και bs είναι φ. Αν φ=0, το R0 παραλείπεται. Αν τα διανύσματα της υπερδομής περνάνε από τα μέσα των διανυσμάτων m|a1| και n|a2| τότε η υπερδομή λέγεται "centered" και συμβολίζεται c(m x n).
To ποσοστό επικάλυψης, θ, ορίζεται ως ο λόγος του αριθμού των προσροφημένων μορίων δια τον αριθμό των διαθέσιμων θέσεων. Θέσεις προσρόφησης είναι πάνω από άτομο της επιφάνειας (on top), μεταξύ δυο επιφανειακών ατόμων (bridge) ή ανάμεσα σε περισότερα επιφανειακά άτομα (hollow). Συνήθως αντιστοιχεί μια διαθέσιμη θέση προσρόφησης ανά επιφανειακό άτομο. Μόρια με ισχυρά κατευθυντικά τροχιακά επιλέγουν συνήθως θέσεις on top (όπως πχ το CO στην Pt(111)), ενώ μόρια με τροχιακά τύπου s επιλέγουν θέσεις με πολλούς γείτονες (πχ Η2 στην Al(100)).
Άσκηση: Κάθε μια από τις δομές στο σχήμα 2.29 από το βιβλίο του Kolasiinski αναπαριστά την κάτοψη επιφανειών του Pt (δομής fcc) με προσροφημένα μόρια CO. Για κάθε μια από αυτές βρείτε (α) ποια επιφάνεια του Pt είναι αυτή; Σε τι είδους θέση (top, bridge, hollow) έχει προσροφηθεί το CO; (β) ποιος είναι ο συμβολισμός Wood για την υπερδομή; (γ) πόσο είναι το ποσοστό επικάλυψης;
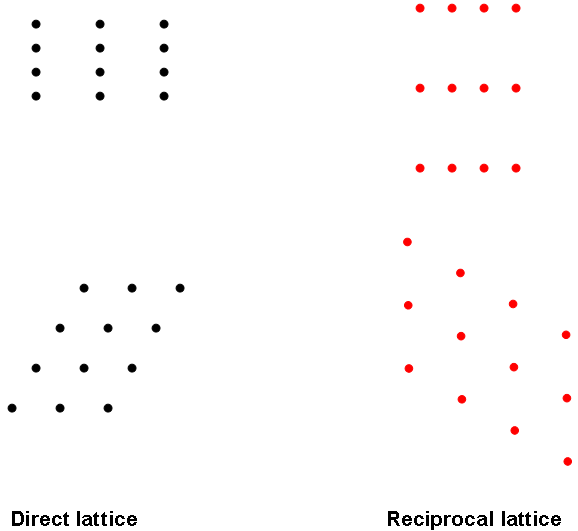 Για να μελετήσουμε τη δομή ενός περιοδικού συστήματος, χρησιμοποιούμε σκέδαση (ηλεκτρονίων, Η/Μ ακτινοβολίας, νετρονίων, ...). Πρέπει το μήκος κύματος της ακτινοβολίας να είναι στην ίδια τάξη μεγέθους με τις αποστάσεις που θέλουμε να μελετήσουμε. Δείξτε ότι αυτό ισχύει για ηλεκτρόνια χαμηλής ενέργειας (~ 10 eV) ή φωτόνια ακτίνων X. Για επιφάνειες προτιμάμε ηλεκτρόνια καθώς είναι πιο εύκολα και επιπλέον δεν διεισδύουν στο εσωτερικό του υλικού. Η τεχνική λέγεται LEED (Low Energy Electron Diffraction). Στην τεχνική αυτή, από μια περιοδική διάταξη από ισοδύναμες γραμμές ατόμων σε απόσταση d, παίρνουμε μια περιοδική διάταξη μεγίστων σε αποστάσεις περίπου α=λR/d, όπου λ το μήκος κύματος και R η απόσταση οθόνης-δείγματος. Έτσι, για κάθε κατεύθυνση στην επιφάνεια, παίρνουμε μια σειρά από κουκίδες στην εικόνα σκέδασης, με αποτέλεσμα να πάρουμε τελικά μια αναπαράσταση της επιφάνειας. Η αναπαράσταση αυτή λέγεται αντίστροφο πλέγμα, γιατί οι αποστάσεις μεταξύ κουκίδων στην εικόνα LEED είναι αντιστρόφως ανάλογες με τις αποστάσεις μεταξύ ισοδύναμων γραμμών ατόμων στην επιφάνεια, σύμφωνα με τον παραπάνω τύπο. Το διπλανό σχήμα δείχνει παραδείγματα αντίστροφων πλεγμάτων.
Υπάρχει και προσομοιωτής LEED. Παραδείγματα πειραμάτων θα βρείτε εδώ.
Για να μελετήσουμε τη δομή ενός περιοδικού συστήματος, χρησιμοποιούμε σκέδαση (ηλεκτρονίων, Η/Μ ακτινοβολίας, νετρονίων, ...). Πρέπει το μήκος κύματος της ακτινοβολίας να είναι στην ίδια τάξη μεγέθους με τις αποστάσεις που θέλουμε να μελετήσουμε. Δείξτε ότι αυτό ισχύει για ηλεκτρόνια χαμηλής ενέργειας (~ 10 eV) ή φωτόνια ακτίνων X. Για επιφάνειες προτιμάμε ηλεκτρόνια καθώς είναι πιο εύκολα και επιπλέον δεν διεισδύουν στο εσωτερικό του υλικού. Η τεχνική λέγεται LEED (Low Energy Electron Diffraction). Στην τεχνική αυτή, από μια περιοδική διάταξη από ισοδύναμες γραμμές ατόμων σε απόσταση d, παίρνουμε μια περιοδική διάταξη μεγίστων σε αποστάσεις περίπου α=λR/d, όπου λ το μήκος κύματος και R η απόσταση οθόνης-δείγματος. Έτσι, για κάθε κατεύθυνση στην επιφάνεια, παίρνουμε μια σειρά από κουκίδες στην εικόνα σκέδασης, με αποτέλεσμα να πάρουμε τελικά μια αναπαράσταση της επιφάνειας. Η αναπαράσταση αυτή λέγεται αντίστροφο πλέγμα, γιατί οι αποστάσεις μεταξύ κουκίδων στην εικόνα LEED είναι αντιστρόφως ανάλογες με τις αποστάσεις μεταξύ ισοδύναμων γραμμών ατόμων στην επιφάνεια, σύμφωνα με τον παραπάνω τύπο. Το διπλανό σχήμα δείχνει παραδείγματα αντίστροφων πλεγμάτων.
Υπάρχει και προσομοιωτής LEED. Παραδείγματα πειραμάτων θα βρείτε εδώ.
Εφαρμογή της ισόθερμης Langmuir
Κομμάτι σιδήρου βρίσκεται σε ισορροπία με αέριο οξυγόνο υπο πίεση P. Μεταβάλλουμε την πίεση και ζυγίζουμε το μέταλλο. Με τέτοιες μετρήσεις, παίρνουμε τον παρακάτω πίνακα τιμών για την πίεση του οξυγόνου και την μάζα που προσροφήθηκε κάθε φορά:
| P (Pa) | m (μgr) |
| 0.28 | 1.40 |
| 0.61 | 2.21 |
| 0.95 | 2.78 |
| 1.70 | 3.23 |
(α) Βρείτε αν στην επιφάνεια του σιδήρου έχουμε μοριακό ή ατομικό οξυγόνο. Για να απαντήσετε, εξετάστε αν ισχύει η εξίσωση θ=KP/(1+KP) (προσρόφηση χωρίς διάσπαση) ή η εξίσωση θ=√(K'P)/(1+√(Κ'P)) (προσρόφηση με διάσπαση). Χρησιμοποιήστε τη σχέση θ=m/m∞. Είναι καλύτερα να δουλέψουμε με σχέσεις της μορφής y=ax+b. Αν είχα μοριακό οξυγόνο, η πρώτη σχέση δίνει (P/m)=(1/m∞K)+(1/m∞)P , δηλαδή y=P/m, x=P. Αντίθετα, αν είχα ατομικό οξυγόνο, η δεύτερη σχέση δίνει (√P/m)=(1/m∞K')+(1/m∞)√P , δηλαδή y=√P/m, x=√P. Φτιάξτε τις δυο γραφικές παραστάσεις. Ποια από τις δυο μοιάζει περισότερο με ευθεία; Τι συμπεραίνετε για το είδος του προσροφημένου οξυγόνου;
(β) Από την σωστή γραφική παράσταση, αυτή δηλαδή που μοιάζει με ευθεία, υπολογίστε την παράμετρο m∞. Εξηγήστε πώς μπορύμε από την παράμετρο αυτή να υπολογίσουμε το εμβαδόν της επιφάνειας, γνωρίζοντας την απόσταση μεταξύ γειτονικών ατόμων.
Κινητική της προσρόφησης και εκρόφησης
Όπως ξέρουμε από τη θερμοδυναμική, κάθε σύστημα προσαρμόζει την κατάστασή του ώστε να ελαχιστοποιεί την ελεύθερη ενέργειά του, G=U+PV-TS U είναι η ενέργεια και S η εντροπία. Δικαιολογήστε το γεγονός ότι στην αέρια φάση τα μόρια έχουν ψηλότερη ενέργεια αλλά και ψηλότερη εντροπία σε σχέση με τα προσροφημένα μόρια. Τι περιμένετε να συμβεί σε πολύ χαμηλές και τι σε πολύ ψηλές θερμοκρασίες;
Οι διαδικασίες προσρόφησης και εκρόφησης (όπως και κάθε χημική αντίδραση) χαρακτηρίζονται από μια ενέργεια ενεργοποίησης (activation energy) δηλαδή το ενεργειακό φράγμα που απαιτείται να υπερπηδηθεί για να γίνει η αντίδραση, και μια θερμότητα (ακριβέστερα, ενέργεια Gibbs) αντίδρασης, η οποία αντιστοιχεί στην διαφορά ενέργειας μεταξύ αντιδρώντων και προϊόντων. Η ενέργεια ενεργοποίησης καθορίζει την ταχύτητα της αντίδρασης (k=k0exp(-Ea/RT) με k0~kBT/h) ενώ η θερμότητα αντίδρασης καθορίζει τη σταθερά της χημικής ισορροπίας (K=exp(-ΔG/RT)).
Temperature Programmed Desorption (TPD)
H ενέργεια ενεργοποίησης για εκρόφηση μετριέται με την τεχνική του Temperature Programmed Desorption (TPD). Στην τεχνική αυτή (α) φέρνουμε σε επαφή, σε χαμηλή θερμοκρασία, την επιφάνεια και το αέριο υπο μελέτη (β) αφήνουμε χρόνο για να ισορροπήσει (γ) αυξάνουμε ομαλά τη θερμοκρασία: Τ=Τ0+κt, όπου κ~2 K/sec. (δ) μετράμε το ρυθμό εκρόφησης (dN/dT) συναρτήσει της θερμοκρασίας. Από τις παραπάνω σχέσεις, μπορούμε να δείξουμε ότι dN/dT=AN/κ exp(-Ed/RT). Η σταθερά Α είναι της τάξεως του 1013. Τι μορφή θα έχει η γραφική παράσταση του dN/dT σαν συνάρτηση της θερμοκρασίας; Αφού η ταχύτητα της αντίδρασης αυξάνεται με τη θερμοκρασία, γιατί το dN/dT μηδενίζεται σε μεγάλες θερμοκρασίες; Μπορούμε να βρούμε την ενέργεια εκρόφησης με δυο κυρίως τρόπους: (α) με διάγραμμα Arrhenius του ln(dN/dT) συναρτήσει του 1/Τ σε χαμηλές θερμοκρασίες, οπότε η κλίση της προκύπτουσας ευθείας θα ισούται με Ed/R. (β) χρησιμοποιώντας το μέγιστο του ρυθμού εκρόφησης. Βρείτε την εξίσωση που ικανοποιεί η θερμοκρασία Tp για την οποία ο ρυθμός εκρόφησης είναι μέγιστος.
Άσκηση: Σε ένα πείραμα TPD o ρυθμός εκρόφησης ήταν 0.012, 0.137 και 1.185 για θερμοκρασία 320Κ, 340Κ και 360Κ, αντίστοιχα. Ο ρυθμός θέρμανσης ήταν 2Κ/s και η θερμοκρασία μέγιστου ρυθμού ήταν Tp=400K. Υπολογίστε την ενέργεια εκρόφησης.
Ο μέσος χρόνος παραμονής ενός μορίου σε μια επιφάνεια εξαρτάται από την ενέργεια που απαιτείται για να εκροφηθεί το μόριο. Ονομάζουμε χημειορρόφηση την περίπτωση όπου ο χρόνος αυτός είναι μεγάλος (οπότε σχηματίζεται χημικός δεσμός μεταξύ του μορίου και της επιφάνειας) και φυσιρρόφηση την περίπτωση όπου ο χρόνος είναι αμελήτέος (οπότε το μόριο απλά ακουμπάει στην επιφάνεια). Δείξτε ότι έχουμε χημιρρόφηση όταν είναι ποερίπου Ed > 50 kJ/mol.
Ενθαλπία προσρόφησης
Η σταθερά K της χημικής ισορροπίας συνδέεται με την ενθαλπία προσρόφησης μέσω της K=exp(-ΔGAD/RT)=K0exp(-ΔHAD/RT) όπου ΔGAD= ΔHAD-ΤΔSAD είναι η διαφορά στην ελεύθερη ενέργεια Gibbs μεταξύ αέριας και προσροφημένης φάσης. Χρησιμοποιείστε τη σχέση αυτή και τη σχέση του Langmuir για να δείξετε ότι lnP=ΔHAD/RT + c, όπου το c δεν εξαρτάται από τα P, T αλλά μόνο από την επιφανειακή συγκέντρωση. Αυτή η σχέση μας επιτρέπει τον προσδιορισμό της ενθαλπίας προσρόφησης μέσω πειράματος όπου μεταβάλλουμε την πίεση και τη θερμοκρασία έτσι ώστε η επιφανειακή συγκέντρωση να μένει σταθερή.
Παράδειγμα: σε ένα πείραμα τοποθετείται οξυγόνο σε πίεση 1 mbar μέσα σε ασημένιο δοχείο στους 700 Κ. Μετράμε ότι προσροφήθηκε κάποια μάζα οξυγόνου. Αν αυξήσουμε τη θερμοκρασία στους 800 Κ, απαιτείται πίεση 36 mbar για να έχουμε προσρόφηση ίδιας μάζας οξυγόνου. Μπορείτε να υπολογίσετε την ενθαλπία προσρόφησης του οξυγόνου στον άργυρο από αυτό το δεδομένο;
Κατάλυση
Όταν έχουμε δυο ή περισσότερα είδη προσροφημένων μορίων στην επιφάνεια, τα ποσοστά επικάλυψης βρίσκονται λύνοντας ένα σύστημα εξισώσεων. Δείτε για παράδειγμα το πρώτο θέμα της τελικής εξέτασης του 2008.Λέγοντας κατάλυση, εννοούμε την επιτάχυνση χημικών αντιδράσεων χρησιμοποιώντας μια ουσία (η οποία λέγεται καταλύτης), η οποία δεν μεταβάλλεται κατά τη διάρκεια της αντίδρασης. Η κατάλυση μπορεί να είναι ομογενής, αν ο καταλύτης βρίσκεται στην ίδια φάση με τα αντιδρώντα (πχ τα ένζυμα που μετατρέπουν το μούστο σε κρασί) ή ετερογενής, αν ο καταλύτης δεν ρίσκεται στην ίδια φάση με τα αντιδρώντα (πχ ο μεταλλικός Pt που οξειδώνει αέριο CO σε CO2 στα αυτοκίνητα). Ο καταλύτης δεν μπορεί να αλλάξει τη θερμότητα της αντίδρασης, και να κάνει πχ μια ενδόθερμη αντίδραση να γίνει εξώθερμη. Μπορεί όμως να αλλάξει τη σταθερά της χημικής ισορροπίας, και άρα την απόδοση της αντίδρασης. Η πιο σημαντική όμως ιδιότητα του καταλύτη είναι ότι αυξάνει, σηνήθως κατά πολλές τάξεις μεγέθους, την ταχύτητα της αντίδρασης, καθώς μειώνει την ενέργεια ενεργοποίησης. Για να πειστείτε, υπολογίστε το λόγο των exp(-E/RT) και exp(-E'/RT) όταν T=300 K και Ε'-Ε=1 eV ~ 100 kJ/mol.
Οι δυο βασικές αρχές της κατάλυσης είναι η αρχή του Langmuir, σύμφωνα με την οποία είναι πολύ πιθανότερο να αντιδράσουν δυο μόρια σε δυο παρά σε τρεις διαστάσεις, και η αρχή του Sabatire, σύμφωνα με την οποία οι καλύτεροι καταλύτες είναι αυτοί που έχουν μέτρια ενέργεια προσρόφησης για τα μόρια των αντιδρώντων (ούτε χαμηλή, οπότε θ~0, αλλά ούτε και υψηλή, οπότε θ*~0).
Για να δούμε πως εξαρτάται η ταχύτητα καταλυόμενης αντίδρασης από τη θερμοκρασία, ας δούμε ένα ρεαλιστικό παράδειγμα, συγκεκριμένα την οξείδωση του CO σε επιφάνεια Pt(111) (παρόμοια ανιδραση γίνεται σε καταλύτες αυτοκινήτου): (στα παρακάτω το σύμβολο PX δηλώνει το λόγο της μερικής πίεσης του Χ προς τη συνολική πίεση)
| CO+*↔CO* | θCO=Κ1PCOθ* | (1) |
| 1/2O2+*↔O* | θO=√(Κ2PO2)θ* | (2) |
| CO*+O*↔CO2*+* | r=k3θCOθO | (3) |
| CO2*↔CO2+* | θCO2=Κ4 PCO2 θ* | (4) |
| Ποσοστά επικάλυψης: | θCO+θCO2+θO+θ*=1 | (5) |
| Νόμος Dalton: | PCO+PO+PCO2=1 | (6) |
Θεωρούμε ότι ένα βήμα (εδώ το (3)) είναι το πιο αργό από όλα, και επομένως αυτό καθορίζει το ρυθμό της συνολικής αντίδρασης. Για την αντίδραση αυτή θα θεωρήουμε ότι πάει μόνο προς τα δεξιά, ενώ οι άλλες αντιδράσεις είναι σε ισορροπία. Αν λύσουμε τις εξισώσεις αυτές και σχεδιάσουμε την ταχύτητα της αντίδρασης σα συνάρτηση της συγκέντρωσης CO στο αέριο και τις θερμοκρασίας (θεωρώντας ότι θCO2~PCO2~0), θα πάρουμε τις παρακάτω καμπύλες, οι οποίες δείχνουν ότι για κάθε καταλύτη και για κάθε αντίδραση υπάρχει συγκεκριμένη περιοχή τιμών πίεσης και θερμοκρασίας στην οποία η απόδοση είναι βέλτιστη. Για αυτό αυτές οι γραφικές παραστάσεις ονομάζονται καμπύλες ηφαιστείου (volcano curves).
Σύνθεση αμμωνίας
H χημική αντίδραση που χρησιμοποιείται περισσότερο από οποιαδήποτε άλλη στον κόσμο είναι η σύνθεση της αμμωνίας από άζωτο και υδρογόνο, υπό υψηλες πιέσεις (100-300 bar) και χρησιμοποιώντας καταλύτες βασισμένους σε μεταβατικά μέταλλα. Η τεχνική αυτή λέγεται σύνθεση Haber-Bosch, και χρησιμοποιείται κυρίως για την παρασκευή λιπασμάτων. Η μέθοδος των Fritz Haber και Carl Bosch ευθύνεται λοιπόν, σε μεγάλο βαθμό, για την τεράστια αύξηση του πληθυσμού της γής μετά το 1920.
To Ν2 έχει τον ισχυρότερο δεσμό που γνωρίζουμε στη φύση, καθώς για να διασπαστεί απαιτούνται περίπου 950 kJ/mol. Αντίθετα, στους σύγχρονους καταλύτες, η ενέργεια ενεργοποίησης για τη διάσπαση του αζώτου είναι μόλις 70 kJ/mol. Από τα δεδομένα αυτά μπορούμε να δείξουμε ότι αν είχαμε όλο το άζωτο της γής και περιμέναμε χρόνο ίσο με την ηλικία του σύμπαντος, η πιθανότητα να συμβεί έστω και μια διάσπαση μορίου αζώτου θα ήταν 1030 φορές μικρότερη από την πιθανότητα να διασπαστεί ένα μόριο αζώτου σε ένα δευτερόλεπτο, αν χρησιμοποιούμε καταλύτη!
Η βιομηχανική σύθεση της αμμωνίας περιλαμβάνει διάφορα στάδια τα οποία καταλήγουν στην απομώνωση του αζώτου (ξεκινώντας από ατμοσφαιρικό αέρα) και του υδρογόνου (ξεκινώντας από φυσικό αέριο). Απαιτούνται μεγάλες ποσότητες νερού, τόσο για τη σύνθεση H2 από το φυσικό αέριο, με αντιδράσεις της μορφής CH4+H2O↔CO+3H2 (steam reforming), όσο και για την απομάκρυνση του παραγόμενου CO μέσω της CO+H2O↔CO2+H2 (water gas shift). Απαιτούνται επίσης τεράστιες ποσότητες ενέργειας για τη θέρμανση και συμπίεση των αερίων: το 1% της παγκόσμιας παραγωγής ενέργειας καταναλώνεται σε μονάδες σύνθεσης αμμωνίας.
O μηχανισμός της σύνθεσης Haber-Bosch περιγράφεται στα παρακάτω βήματα.
| N2+*↔N2* | (1) |
| N2*+*↔2N* | (2) |
| N*+H*↔NH*+* | (3) |
| NH*+H*↔NH2*+* | (4) |
| NH2*+H*↔NH3*+* | (5) |
| NH3*↔NH3+* | (6) |
| H2+2*↔2H* | (7) |

