-
Mε βάση τη νόμο του Moore(
ο αριθμός των τρανζίστορ που χωράνε σε ένα τσιπ διπλασιάζεται κάθε δυο χρόνια)
και τη γραφική του παράσταση: α) εκτιμήστε το μέγεθος κάθε τρανζίστορ στον Pentium 4 (P4) και β) εκτιμήστε ποιο έτος έχουμε τρανζίστορ μεγέθους 10nm.
- Εκτιμήστε πόσα άτομα χρησιμοποιούνται για την αποθήκευση 1 bit πληροφορίας σε ένα
(α) cd-rom (β) dvd-rom (γ) usb flash stick. Πάρτε εύλογες εκτιμήσεις για το εμβαδόν, τη χωρητικότητα και όποιες άλλες
παραμέτρους χρειαστέιτε.
- Θεωρώντας ότι χρειάζονται τουλάχιστον 1000 άτομα για να αποθηκευτεί ένα bit πληροφορίας, υπολογίστε τη
μέγιστη χωρητικότητα που μπορεί να έχει ένας συμβατικός μεταλλικός σκληρός δίσκος διαμέτρου 3.5 ιντσών.
- Νανοϋλικό που χρησιμοποιείται για αποθήκευση δεδομένων περιέχει 99% κατά βάρος κεραμικό και
1% κατά βάρος νανοσωματίδια Fe. Τα νανοσωματίδια είναι κύβοι πλευράς 80 nm.
Υπολογίστε πόση μάζα αυτού του υλικού απαιτείται για να φτιαχτεί μνήμη 1 GB εάν εγγράφεται 1 bit σε κάθε νανοσωματίδιο.
O Fe έχει ατομικό βάρος 56 g/mol και κρυσταλλώνεται σε δομή bcc με πλεγματική σταθερά
2.9 Å.
-
 Η διπλανή γραφική παράσταση δείχνει τη χωρητικότητα (σε GB) του μεγαλύτερου σκληρού δίσκου της αγοράς για κάθε χρονιά σε διάφορα είδη υπολογιστών.
Παίρνοντας εύλογες εκτιμήσεις, και με βάση την ευθεία του διαγράμματος, φτιάξτε μια πρόχειρη γραφική παράσταση του αριθμού ατόμων που απαιτείται για εγγραφή 1 bit πληροφορίας σαν συνάρτηση του χρόνου.
Η διπλανή γραφική παράσταση δείχνει τη χωρητικότητα (σε GB) του μεγαλύτερου σκληρού δίσκου της αγοράς για κάθε χρονιά σε διάφορα είδη υπολογιστών.
Παίρνοντας εύλογες εκτιμήσεις, και με βάση την ευθεία του διαγράμματος, φτιάξτε μια πρόχειρη γραφική παράσταση του αριθμού ατόμων που απαιτείται για εγγραφή 1 bit πληροφορίας σαν συνάρτηση του χρόνου.
Οι βασικές φυσικές ιδιότητες που χαρακτηρίζουν τα νανοϋλικά
- Ο σίδηρος φτιάχνει δομή bcc με πλεγματική σταθερά α=0.287 nm. Θεωρήστε σιδερένιο κύβο ακμής L ο οποίος έχει έδρες παράλληλες στις έδρες της θεμελιώδους κυψελίδας. Θεωρήστε ότι η διάμετρος του ατόμου ισούται με την απόσταση γειτονικών ατόμων στην δομή bcc.
Υπολογίστε το λόγο, χ, του αριθμού επιφανειακών ατόμων προς τον συνολικό αριθμό ατόμων στον κύβο για χαρακτηριστικές τιμές του L (1 nm, 10 nm, 1μm, 1mm, 1cm).
-
Η ειδική επιφάνεια ορίζεται ως το πηλίκο της επιφάνειας ενός υλικού δια τη μάζα του. Υπολογίστε την ειδική επιφάνεια του Rh στις παρακάτω μορφές:
- Σφαιρίδια Rh διαμέτρου 0.5 cm.
- Φύλλα Rh πάχους 200 μm.
- Κυβικά νανοσωματίδια Rh ακμής 10 nm.
Για να λειτουργήσει καλά ο καταλύτης ενός αυτοκινήτου, χρειάζεται τουλάχιστον 0.1 m2 Rh. Υπολογίστε το κόστος του απαιτούμενου Rh σε κάθε μία από τις παραπάνω περιπτώσεις. Η πυκνότητα του Rh είναι 12.5 g/cc, και η τιμή του 180 euro/g.
- Θεωρήστε ένα νανοσωματίδιο με όγκο V. Ορίζουμε το μέγεθός του, d, από την σχέση V=d3. Έστω ότι το άθροισμα των μηκών όλων των ακμών είναι D και το συνολικό εμβαδόν του νανοσωματιδίου είναι A. Ορίζουμε τις σταθερές L και S από τις σχέσεις D=Ld και A=Sd2. Φτιάξτε πίνακα με τις τιμές των S και L για τον κύβο, το σχήμα του παραδέιγματος παρακάτω και για ακόμα έξι σχήματα που θα βρείτε στο διαδίκτυο.
Παράδειγμα: στο κανονικό κόλουρο οκτάεδρο είναι V=11.31α3=d3 άρα d=2.24a. To εμβαδόν A=26.78a2=5.34 d^2 και το νανοσωματίδιο έχει 36 ακμές, άρα D=36a=16.07d. Επομένως για αυτό το σχήμα είναι S=5.34 και L=16.07. Ένα παράδειγμα χρήσης των S και L στις ιδιότητες νανοϋλικών μπορείτε να δείτε εδώ (σελ. 82).
-
- Υπολογίστε την ειδική επιφάνεια (σε m2/g) των παρακάτω σιδερένιων σωμάτων: (α) κύβος πλευράς c nm. (b) σφαίρα ακτίνας b nm. (c) κανονικό κόλουρο οκτάεδρο πλευράς a nm. Δίνεται η πυκνότητα του Fe, ρ = 7.9 g/cm3. Βρείτε τους τύπους για τον όγκο και το συνολικό εμβαδόν του (c) στην wikipedia
-
Βρείτε τις τιμές των a, b, c ώστε να έχουμε ειδική επιφάνεια ίση με 100 m2/g.
- Βρείτε τις τιμές των a και b σαν συνάρτηση του c, ώστε τα τρία σχήματα να έχουν ίσο όγκο. Ποιο σχήμα έχει την μικρότερη και ποιο την μεγαλύτερη ειδική επιφάνεια όταν έχουν όλα τον ίδιο όγκο;
- Ηλεκτρόνιο το οποίο κινείται σε νανοκαλώδιο μήκους L και αμελητέου πάχους μεταπίπτει από την τρίτη διεγερμένη στάθμη στην δεύτερη διεγερμένη στάθμη εκπέμποντας ένα φωτόνιο μήκους κύματος 120 nm. Βρείτε το μήκος κύματος του φωτονίου που θα εκπέμπονταν αν η μετάπτωση γινόταν (α) στην πρώτη διεγερμένη και (β) στη θεμελιώδη στάθμη.
- Πρωτόνιο και ηλεκτρόνιο κινούνται σε όμοια καλώδια μήκους L και αμελητέου πάχους, και
βρίσκονται το καθένα στην θεμελιώση του κατάσταση. Ποιο από τα δυο θα έχει χαμηλότερη ενέργεια, και ποιος
θα είναι ο λόγος των ενεργειών τους;
- Ηλεκτρόνιο κινείται σε καλώδιο μήκους L και αμελητέου πάχους μεταπίπτει από την δεύτερη διεγερμένη στάθμη στην πρώτη διεγερμένη στάθμη εκπέμποντας ένα φωτόνιο μήκους κύματος 120 nm. Στη συνέχεια μεταπίπτει από την πρώτη διεγερμένη
στη θεμελιώδη στάθμη, εκπέμποντας ακόμα ένα φωτόνιο. Υπολογίστε το μήκος κύματός του.
- Μια προσέγγιση της κίνησης ηλεκτρονίων σε μακρομόρια είναι να θεωρήσουμε
ότι κινούνται ανεξάρτητα και με αμελητέες απώσεις Coulomb σε πολύ
λεπτό σωλήνα μήκους L, όπου L είναι το μήκος του μορίου. Χρησιμοποιήστε την προσέγγιση αυτή
για να υπολογίσετε, σε eV, τις ενέργειες για τις κατειλημένες και τις δυο πρώτες κενές στάθμες των
ηλεκτρονίων σε θερμοκρασία T=0, καθώς και την ενέργεια Fermi στο οκτάνιο. Θεωρήστε δυο
ηλεκτρόνια σθένους για κάθε άτομο C και ότι οι αποστάσεις μεταξύ
ατόμων C είναι 0.15 nm.
- Χρησιμοιποιείστε τη θεωρία της προηγούμενης άσκησης για να υπολογίσετε
το μήκος κύματος της ακτινοβολίας την οποία μπορεί να αποροφήσει το μόριο
H2C=C-CH=...-C=CH2, το οποίο περιέχει n άτομα άνθρακα με εναλλάξ απλούς και διπλούς δεσμούς.
Κάθε άτομο έχει ένα ηλεκτρόνιο σθένους, και οι αποστάσεις μεταξύ
ατόμων C είναι 0.15 nm. Βρείτε τις τιμές του n για τις οποίες το μόριο μπορεί να αποροφήσει φωτόνια ορατού φωτός.
Σε ποια χρώματα αντιστοιχούν; Τα χρώματα αυτά σχετίζονται με τα χρώματα που θα έχουν οι αντίστοιχες χημικές ουσίες. Γιατί;
- Θεωρήστε ένα επίπεδο πυκνωτή αποτελούμενο από δυο τετράγωνες μεταλλικές πλάκες πλευράς L,
οι οποίες απέχουν L/10 μεταξύ τους. (α) Δείξτε ότι η χωρητικότητα του συστήματος είναι C=10ε0L (ξεκινήστε από τον ορισμό, C=Q/V).
(β) Η πιθανότητα να φορτιστεί ο πυκνωτής με το ελάχιστο δυνατό φορτίο, δηλαδή ένα ηλεκτρόνιο, δίνεται από τον τύπο
P=exp(-E/kT), όπου E είναι η ενέργεια που έχει το σύστημα (E=e2/2C), k η σταθερά του Boltzmann
και Τ η θερμοκρασία. Υπολογίστε την πιθανότητα αυτή σαν συνάρτηση του L, για θερμοκρασία δωματίου.
Τι τιμή έχει σε ένα τυπικό πυκνωτή (L=1 mm) και τι σε ένα νανοσύστημα (L=10 nm);
- Η πιθανότητα να φορτιστεί κάποιο σώμα με το ελάχιστο δυνατό φορτίο, δηλαδή ένα ηλεκτρόνιο, δίνεται από τον τύπο P=exp(-E/kT), όπου E είναι η ενέργεια που έχει το σύστημα (E=e2/2C), k η σταθερά του Boltzmann, Τ η θερμοκρασία και C η χωρητικότητα του σώματος. Υπολογίσετε την πιθανότητα να φορτιστεί μια μεταλλική σφαίρα ακτίνας R με φορτίο e σε θερμοκρασία δωματίου. Σχεδιάστε την συνάρτηση P=f(R) για τιμές του R από 1 nm έως 1 μm. Βρείτε για ποιές τιμές του R η πιθανότητα είναι (α) μεγαλύτερη από
99% και (β) μικρότερη από 1%.
- Η πιθανότητα να φορτιστεί ένα σύστημα (σε ισορροπία) με φορτίο e δίνεται από τη σχέση P=exp(-E/kT), όπου
E=e2/2C. Στους τύπους αυτούς T είναι η
θερμοκρασία, k=R/NA η σταθερά του Boltzmann, και C η χωρητικότητα του
συστήματος. (α) Εξηγήστε γιατί η πιθανότητα P που ορίσαμε παραπάνω θα είναι κοντά στο 1
για πολύ μακροσκοπικά συστήματα και θα μικραίνει καθώς μικραίνει το μέγεθος
του συστήματος έως ότου γίνει πολύ μικρή όταν φτάσουμε στο ατομικό επίπεδο. Τι
εφαρμογές έχει αυτή η ιδιότητα των νανοϋλικών? (β) Για κάποιο κυβικό νανοσωμάτιο ισχύει C=ε0d/10. Υπολογίστε το
d για το οποίο η πιθανότητα P είναι ίση με 1/2.
-
Nανοσωματίδιο ZnO ακτίνας R=10 nm περιέχει 10 ελεύθερα ηλεκτρόνια λόγω προσμίξεων. Οι επιτρεπόμενες ενέργειες ηλεκτρονίου σε σφαιρικό νανοσωματίδιο δίνονται από τη σχέση:
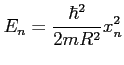 .
.
Είναι x1=3.1, x2=4.5, x3=5.8, x4=6.3, x5=7.0, x6=7.7,
x7=8.2, x8=9.1, x9=9.4. Οι στάθμες αυτές είναι εκφυλισμένες (υπάρχουν πολλές καταστάσεις με ίδια ενέργεια) με βαθμούς εκφυλισμού g1=1, g2=3, g3=5, g4=1, g5=7, g6=3,
g7=9, g8=1.
(α) Υπολογίστε σε eV, τις ενέργειες των 10 ηλεκτρονίων, καθώς και τις δυο χαμηλότερες ενέργειες κενών καταστάσεων.
(β) Υπολογίστε το μέγιστο μήκος κύματος ηλεκτρομαγνητικής ακτινοβολίας που μπορεί να απορροφήσει το νανοσωμάτιο.
-
Θεωρήστε ένα νανοκύλινδρο μήκους L=500nm και μικρής ακτίνας, ο οποίος περιέχει N ηλεκτρόνια. Θεωρήστε ότι
N=L/(2 aB) >> 1.
(α) Χρησιμοποιώντας κλασσικό ηλεκτρομναγνητισμό, βρείτε την ενέργεια που πρέπει να δώσουμε για να φορτιστεί το σύστημα με 1 επιπλέον ηλεκτρόνιο. Σας δίνεται η χωρητικότητα C=2ε0L.
(β) Χρησιμοποιώντας κβαντομηχανική, βρείτε και πάλι την ενέργεια που πρέπει να δώσουμε για να φορτιστεί το σύστημα με 1 επιπλεόν ηλεκτρόνιο.
-
Δυο νανοκαλώδια έχουν ίδιο μήκος, L. Το πρώτο έχει 50 ηλεκτρόνια με ενεργό μάζα m. Το δεύτερο έχει 40 ηλεκτρόνια με ενεργό μάζα 1.2m. Το πρώτο νανοκαλώδιο απορροφά φως μήκους κύματος 700 nm. Βρείτε σε τί μήκος κύματος απορροφά το δεύτερο.
-
Μονοδιάστατο νανοκαλώδιο έχει μήκος 10 nm και περιέχει 12 ελεύθερα ηλεκτρόνια.
- Υπολογείστε την συνολική ενέργεια του συστήματος των ηλεκτρονίων σε eV.
- Υπολογίστε την δύναμη που ασκείται από τα ηλεκτρόνια, F=-dE/dL.Ασκώντρας πίεση στο υλικό, θα είναι πιο εύκολο να κοντύνει ή να μακρύνει το νανοκαλώδιο;
Ατομική δομή στερεών επιφανειών
-
Για τις παρακάτω επιφάνειες: (α) Σχεδιάστε την ατομική δομή τους, δείχνοντας τα άτομα του επιφανειακού επιπέδου καθώς και εκείνα του αμέσως παρακάτω.
(β) Βρείτε τα διανύσματα βάσης, σχεδιάστε τα και υπολογίστε τις x- και y-συνιστώσες τους.
(γ) Υπολογίστε την επιφανειακή συγκέντρωση, ns και το εμβαδόν ανά άτομο, Aat.
(δ) Υπολογίστε την πλήρωση, f.
(ε) Εκτιμήστε την επιφανειακή τάση (σε J/m2) μετρώντας τον αριθμό των ακόρεστων δεσμών και θεωρώντας ότι κάθε mol ακόρεστων δεσμών στοιχίζει ενέργεια Ecoh/z όπου
Ecoh είναι η ενέργεια συνοχής του στερεού και
z ο αριθμός γειτόνων κάθε ατόμου στο εσωτερικό.
- Fe(100) (O Fe σχηματίζει κρύσταλλο δομής
bcc
με πλεγματική σταθερά a=0.287 nm και έχει Ecoh=414 kJ/mol).
- Si(110) (To Si σχηματίζει κρύσταλλο δομής
διαμαντιού
με πλεγματική σταθερά a=0.543 nm και έχει Ecoh=450 kJ/mol).
- Cu(110) (O Cu σχηματίζει κρύσταλλο δομής
fcc
με πλεγματική σταθερά a=0.361 nm και έχει Ecoh=337 kJ/mol).
- Cu(111) (O Cu σχηματίζει κρύσταλλο δομής
fcc
με πλεγματική σταθερά a=0.361 nm και έχει Ecoh=337 kJ/mol).
- Mg(001) (To Mg σχηματίζει κρύσταλλο δομής
hcp
με πλεγματικές σταθερές a=0.321 nm και c=0.521 nm και έχει Ecoh=147 kJ/mol).
- Ti(001) (To Ti σχηματίζει κρύσταλλο δομής
hcp
με πλεγματικές σταθερές a=0.295 nm και c=0.466 nm και έχει Ecoh=473 kJ/mol).
- Na(110) (To Na σχηματίζει κρύσταλλο δομής
bcc
με πλεγματική σταθερά a=0.429 nm και έχει Ecoh=108 kJ/mol).
- Al(100) (To Al σχηματίζει κρύσταλλο δομής
fcc
με πλεγματική σταθερά a=0.405 nm και έχει Ecoh=330 kJ/mol).
- Υπολογίστε την πίεση αερίου αργού που απαιτείται ώστε να έχουμε 4.5 1020 συγκρούσεις ανά sec
πάνω σε κυκλική επιφάνεια διαμέτρου 2 mm στους 525 Κ.
- Το Ni σχηματίζει δομή fcc με πλεγματική σταθερά a=0.352 nm. Υπολογίστε πόσα μόρια συγκρούονται με κάθε άτομο της επιφάνειας (111) ανά δευτερόλεπτο μέσα σε ένα δοχείο που περιέχει (α) υδρογόνο ή (β) προπάνιο στους 298 Κ και με την πίεση να είναι (i) 100 Pa ή (ii) 0.10 μTorr.
- Υπολογίστε το χρόνο που απαιτείται για να σχηματιστεί 1 ML CO στην επιφάνεια Pt(111) στους 200Κ υπό πίεση 1 Torr. Ο Pt έχει δομή fcc με πλεγματική σταθερά a=0.392 nm.
- To Mo έχει δομή bcc με πλεγματική σταθερά a=0.315 nm. Υδρογόνο προσροφάται στην επιφάνεια Mo(110) με διάσπαση,
δηλαδή από κάθε μόριο Η2 από την αέρια φάση προκύπτουν δυο προσροφημένα άτομα Η. Η πίεση είναι 10-9 Torr και η θερμοκρασία 300 Κ. Υπολογίστε σε πόσο χρόνο θα έχει προσροφηθεί 0.5 ML.
-
To V φτιάχνει δομή bcc με πλεγματική σταθερά a=3.03 Å. Οξυγόνο προσροφάται στην επιφάνεια (110) με
διάσπαση, δηλαδή από κάθε μόριο O2 από την αέρια φάση προκύπτουν δυο
προσροφημένα άτομα O. Η πίεση είναι 10-9 Pa και η
θερμοκρασία 300 Κ. (α) Υπολογίστε σε πόσο χρόνο θα έχει προσροφηθεί 0.25 ML
(δηλαδή το 1/4 των θέσεων της επιφάνειας καταλαμβάνονται από
προσροφημένα Ο). (β) Αν η επιφάνεια έχει εμβαδόν 100 cm2, πόσο θα
έχει αυξηθεί η μάζα του λόγω της παραπάνω προσρόφησης;
-
O Fe σχηματίζει δομή bcc με πλεγματική σταθερά a=0.287 nm. Υπολογίστε πόσα μόρια συγκρούονται με κάθε άτομο της επιφάνειας (110) ανά δευτερόλεπτο μέσα σε ένα δοχείο που περιέχει αιθάνιο στους 100 Κ και σε 100 Pa. Ελάχιστα από τα προσροφημένα μόρια αιθανίου εγκαταλείπουν την επιφάνεια όταν είναι παγωμένη, ενώ αντίθετα σχεδόν όλα θα εκροφηθούν αν αυξήσουμε πολύ τη θερμοκρασία. Πώς το εξηγείτε;
-
Το Πυρίτιο κρυσταλλώνεται σε δομή διαμαντιού (πλέγμα με διατομική βάση στις θέσεις (0,0,0) και (a/4, a/4, a/4).
- Σχεδιάστε την επιφάνεια (100), και δώστε τύπους για το ποσοστό πλήρωσης, την επιφανειακή τάση και την συγκέντρωση επιφανειακών ατόμων.
- Εκτιμήστε την τάξη μεγέθους των δυο τελευταίων ποσοτήτων.
- Σχεδιάστε τις θεμελιώδεις κυψελίδες για υπερδομές (2×1), (2×2) και c(4×4).
-
 Στο διπλανό σχήμα, η διαφορά στην ενέργεια της δεξιάς και αριστερής επιφάνειας (ίδιο υλικό, ίδιο εμβαδόν κάτοψης) είναι EsL, όπου Es η ενέργεια σκαλοπατιού.
(α) Εκτιμήστε την τάξη μεγέθους της ενέργειας σκαλοπατιού σε μέταλλα και για μονοατομικό σκαλοπάτι, δηλαδή με ύψος μόλις ενός ατόμου. (β) Εξηγήστε γιατί η ενέργεια μονοατομικού σκαλοπατιού εξαρτάται και από το υλικό αλλά και από τον προσανατολισμό του σκαλοπατιού πάνω στην επιφάνεια.
Στο διπλανό σχήμα, η διαφορά στην ενέργεια της δεξιάς και αριστερής επιφάνειας (ίδιο υλικό, ίδιο εμβαδόν κάτοψης) είναι EsL, όπου Es η ενέργεια σκαλοπατιού.
(α) Εκτιμήστε την τάξη μεγέθους της ενέργειας σκαλοπατιού σε μέταλλα και για μονοατομικό σκαλοπάτι, δηλαδή με ύψος μόλις ενός ατόμου. (β) Εξηγήστε γιατί η ενέργεια μονοατομικού σκαλοπατιού εξαρτάται και από το υλικό αλλά και από τον προσανατολισμό του σκαλοπατιού πάνω στην επιφάνεια.
- Για την επιφάνεια Mg(001): (α) Σχεδιάστε την ατομική δομή της, δείχνοντας τα άτομα του επιφανειακού επιπέδου καθώς και εκείνα του αμέσως παρακάτω. (β) Βρείτε τα διανύσματα βάσης, σχεδιάστε τα και υπολογίστε τις x και yσυνιστώσες τους. (γ) Υπολογίστε την επιφανειακή συγκέντρωση, ns. (δ) Υπολογίστε την πλήρωση, f. (ε) Υπολογίστε την επιφανειακή τάση (σε J/m2) σύμφωνα με το μοντέλο σπασμένων δεσμών. To Mg σχηματίζει κρύσταλλο δομής hcp με πλεγματικές σταθερές a=0.321 nm και c=0.521 nm και έχει ενέργεια συνοχής 147 kJ/mol).
- Tο AlCo κρυσταλλώνεται σε δομή CsCl. Το στερεό Al έχει δομή fcc με a=0.405 nm και ενέργεια συνοχής 3.39 eV/άτομο. Το στερεό Co έχει δομή hcp με a=0.251 nm, c=0.407 nm και ενέργεια συνοχής 4.39 eV/άτομο. Με βάση τα παραπάνω:
Eκτιμήστε την πλεγματική σταθερά και την ενέργεια συνοχής του AlCo.
Xρησιμοποιώντας το μοντέλο των σπασμένων δεσμών, υπολογίστε την επιφανειακή τάση των AlCo(100) και AlCo(110).
-
Εκτιμήστε την επιφανειακή τάση για τις (100), (110) και (111) του Fe, ο οποίος έχει δομή bcc με a=0.287nm και ενέργεια συνοχής Ec=414 kJ/mol. Τί σχήμα περιμένετε να έχουν τα νανοσωμάτια Fe;
-
To Na σχηματίζει κρύσταλλο δομής bcc με πλεγματική σταθερά a=0.429 nm και έχει Ecoh = 108 kJ/mol. Υπολογίστε (α) τo ποσοστό πλήρωσης και (β) την επιφανειακή τάση των επιφανειών Na(100) και Na(110).
-
Υπολογίστε το εμβαδόν ανά άτομο και την πλήρωση στις επιφάνειες Al(100), Au(100), Ni(100). Πάρτε πληροφορίες για την δομή του κάθε μετάλλου από το webelements.
-
Εκτιμήστε πρόχειρα πόσα μόρια του αέρα απαιτούνται για να καλυφθεί
πλήρως το τζάμι ενός παραθύρου. Επίσης, εκτιμήστε πρόχειρα πόσος χρόνος απαιτείται
για να χτυπήσουν αυτά τα μόρια το τζάμι σε κανονικές συνθήκες. Πάρτε εύλογες εκτιμήσεις
ή προσεγγίσεις των ποσοτήτων που θα χρειαστείτε.
-
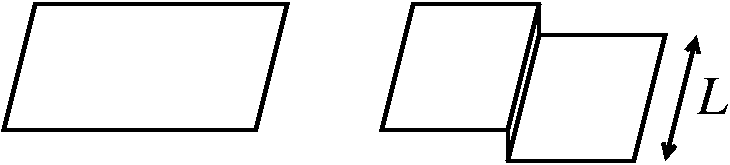
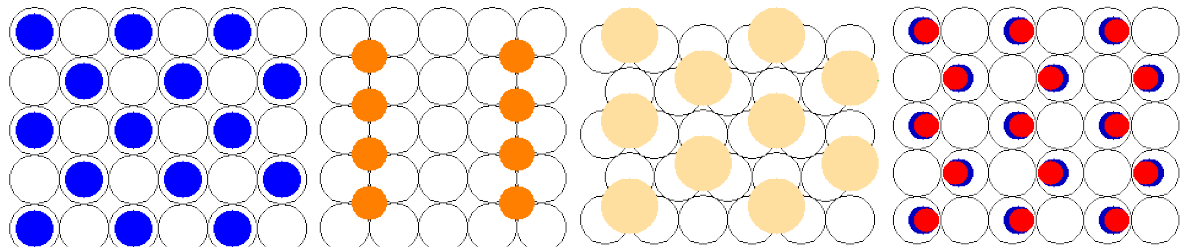
 Υπολογίστε την πλήρωση (f=εμβαδόν ατόμων διά συνολικό εμβαδόν) για την επιφάνεια (110) δομής (α) ClCs και (β) NaCl. Θεωρήστε ότι και στις δυο δομές, τα άτομα είναι ίσες σφαίρες που εφάπτονται.
Υπολογίστε την πλήρωση (f=εμβαδόν ατόμων διά συνολικό εμβαδόν) για την επιφάνεια (110) δομής (α) ClCs και (β) NaCl. Θεωρήστε ότι και στις δυο δομές, τα άτομα είναι ίσες σφαίρες που εφάπτονται.
Σχήμα των νανοσωματιδίων και επιφανειακές τάσεις
- Εκτιμήστε την επιφανειακή τάση για τις (100), (110) και (111) του Fe, ο οποίος έχει δομή bcc με a=0.287nm και ενέργεια συνοχής Ec=414 kJ/mol.
Τί σχήμα περιμένετε να έχουν τα νανοσωμάτια σιδήρου;
- Συγκρίνετε την επιφανειακή τάση για την Fe(210) και την Fe(100). Επιβεβαιώστε ότι η επιφανειακή τάση αυξάνεται όσο μεγαλώνουν οι δείκτες Miller. O Fe έχει δομή bcc με a=0.287nm και ενέργεια συνοχής Ec=414 kJ/mol.
- Υπολογίστε (σε J/m2) τις επιφανειακές τάσεις γ111, γ110 και γ100 για το στερεό Al (ή Au ή Νi, ή Pd ή ...). Βρείτε τις παραμέτρους που θα χρειαστείτε από βιβλία ή το web.
- Εκτιμήστε το σχήμα που θα έχουν οι κρύσταλλοι του κοινού αλατιού, NaCl. Η πλεγματική σταθερά είναι 0.236 nm. Οι ενέργειες συνοχής του
στερεού Na και του μορίου Cl2 είναι 108 kJ/mol και 121 kJ/mol, αντίστοιχα.
- Υπολογίστε (σε J/m2) τις επιφανειακές τάσεις γ110 και γ100 για to στερεό FeO (δομής NaCl). Βρείτε τις παραμέτρους που θα χρειαστείτε από βιβλία ή το web.
- Θεωρήστε ότι έχουμε ένα νανοσωματίδιο από υλικό το οποίο φτιάχνει κρυσταλλική δομή με κυβική συμμετρία. Γνωρίζουμε ότι η (111) είναι η έδρα με τη χαμηλότερη επιφανειακή τάση. Στην περίπτωση που οι άλλες έδρες (hkl) έχουν επιφανειακές τάσης πολύ υψηλότερες από την (111), το σχήμα ελάχιστης ενέργειας για το νανοσωματίδιο θα είναι κανονικό οκτάεδρο. Δείξαμε στη θεωρία ότι για να μην είναι το σχήμα κανονικό οκτάεδρο, και να εμφανιστούν έδρες τύπου (110), θα πρέπει γ110 < √3/√2 γ111. Δείξτε ότι:
- Για να εμφανιστούν έδρες τύπου (100), θα πρέπει γ100 < √3 γ111.
- Για να εμφανιστούν έδρες τύπου (210), θα πρέπει γ210 < 2√3/√5 γ111.
- Για να εμφανιστούν έδρες τύπου (221), θα πρέπει γ221 < 2/√3 γ111.
- Για να εμφανιστούν έδρες τύπου (211), θα πρέπει γ211 < √2 γ111.
- Επαναλάβετε την προηγούμενη άσκηση, θεωρώντας ότι αυτή τη φορά η (100) είναι η επιφάνεια με τη χαμηλότερη επιφανειακή τάση, οπότε το σχήμα ελάχιστης ενέργειας θα είναι κύβος. Βρείτε τις συνθήκες που πρέπει να ικανοποιούν οι επιφανειακές τάσεις τους ώστε να εμφανιστούν έδρες τύπου (110), (111) και (210).
- Η διεπιφανεική τάση μετριέται συνήθως μέσω της γωνίας επαφής.
Υπολογίστε την διεπιφανειακή τάση μεταξύ νερού και των πολυμερών PVC (Poly (vinyl chloride)), PTFE (Poly(tetrafluoroethylene), teflon)
και PS (Polystyrene). Βρείτε τις γωνίες επαφής από εδώ και τις επιφανειακές τάσεις από εδώ. Η επιφανειακή τάση του νερού είναι 0.073 J/m2.
- Σε κάποιο υλικό δομής fcc, γνωρίζουμε ότι η επιφάνεια με τη
χαμήλότερη επιφανειακή τάση είναι η (100). α) Τι μπορείτε να πείτε για το σχήμα ελάχιστης ενέργειας των νανοσωματιδίων
του υλικού αυτού; β) Βρείτε τη συνθήκη που πρέπει να ικανοποιεί η επιφανειακή τάση της (110)
ώστε να εμφανίζονται επιφάνειες τύπου (110) στο παραπάνω σχήμα ελάχιστης
ενέργειας.
-
 Σε ένα πείραμα βρέθηκε ότι νανοσωμάτια Ag τα οποία είχαν αφεθεί να
φτιάξουν το σχήμα ελάχιστης ενέργειας, είχαν σχήμα όπως αυτό της διπλανής
εικόνας. Τι συμπεράσματα μπορείτε να βγάλετε για τις επιφανειακές τάσεις του
αργύρου;
Σε ένα πείραμα βρέθηκε ότι νανοσωμάτια Ag τα οποία είχαν αφεθεί να
φτιάξουν το σχήμα ελάχιστης ενέργειας, είχαν σχήμα όπως αυτό της διπλανής
εικόνας. Τι συμπεράσματα μπορείτε να βγάλετε για τις επιφανειακές τάσεις του
αργύρου;
-
Ο Β. Φρανγκλίνος έγραφε το 1773: "Αν ρίξουμε μια σταγόνα λάδι [..]
πάνω σε οριζόντιο καθρέπτη, η σταγόνα παραμένει στη θέση της, και απλώνεται
ελάχιστα. Αν την ρίξουμε σε νερό, απλώνεται αμέσως καταλαμβάνοντας μεγάλη
έκταση, και φτιάχνοντας ένα υμένιο τόσο λεπτό ώστε δεν φαίνεται καν. Γίνεται
αντιληπτό μόνο από τον ιριδισμό του καθώς ανακλά το φώς.''
Μπορείτε να εξηγήσετε το φαινόμενο? Μπορείτε να εκτιμήσετε πόσο εμβαδόν μπορεί
να καταλαμβάνει μια απλωμένη σταγόνα λαδιού πάνω σε απολύτως ήρεμη επιφάνεια
νερού; Δίνονται οι επιφανειακές και διεπιφανειακές τάσεις:
γνερ=0.073 J/m2,
γλαδ=0.036 J/m2,
γκαθ=0.047 J/m2,
γintλαδ-καθ=0.030 J/m2,
γintλαδ-νερ=0.023 J/m2.
-
Εκτιμήστε το σχήμα ελάχιστης ενέργειας για νανοσωματίδια MgO. Το υλικό αυτό έχει δομή NaCl με πλεγματική σταθερά 0.21 nm.
Οι ενέργειες συνοχής του στερεού Mg και του μορίου O2 είναι 147 kJ/mol και 250 kJ/mol, αντίστοιχα.
-
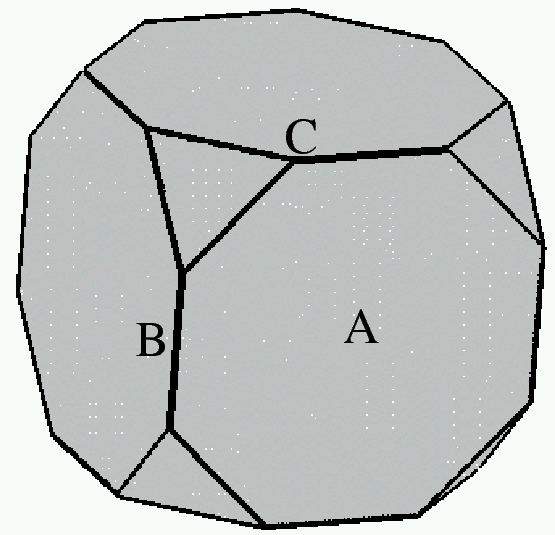 Κάποιο μέταλλο φτιάχνει κρυσταλλική δομή με κυβική συμμετρία. Η επιφάνεια (100) έχει τη χαμηλότερη επιφανειακή τάση, και η (111) έχει επιφανειακή τάση μεγαλύτερη κατά 40%, δηλαδή γ111=1.4γ100. Όλες οι άλλες έδρες (hkl) μπορούν να αγνοηθούν. Το σχήμα δείχνει ένα νανοσωματίδιο αυτού του μετάλλου (Α=κέντρο έδρας, Β=μέσον ακμής, C=κορυφή).
Υπολογίστε το λόγο AB/AC.
Κάποιο μέταλλο φτιάχνει κρυσταλλική δομή με κυβική συμμετρία. Η επιφάνεια (100) έχει τη χαμηλότερη επιφανειακή τάση, και η (111) έχει επιφανειακή τάση μεγαλύτερη κατά 40%, δηλαδή γ111=1.4γ100. Όλες οι άλλες έδρες (hkl) μπορούν να αγνοηθούν. Το σχήμα δείχνει ένα νανοσωματίδιο αυτού του μετάλλου (Α=κέντρο έδρας, Β=μέσον ακμής, C=κορυφή).
Υπολογίστε το λόγο AB/AC.
- Το Po έχει ενέργεια συνοχής 200 kJ/mol και κρυσταλλώνεται σε απλή κυβική δομή με πλεγματική σταθερά a=0.33 nm.
(α) Υπολογίστε τις επιφανειακές τάσεις γ100, γ110, γ210, γ111 σε J/m2.
(β) Βρείτε ποιες από τις παραπάνω επιφάνειες (και γιατί) θα εμφανίζονται στο σχήμα ελάχιστης ενέργειας νανοσωματιδίων .
-
Οι επιφανειακές τάσεις ενός υλικού με τετραγωνική κρυσταλλική δομή είναι γ100= γ010 = 0.16 J/m2, γ110 = 0.18 J/m2 και
γ210= γ120 = 0.18 J/m2 Όλες οι άλλες έδρες έχουν πολύ μεγαλύτερες επιφανειακές τάσεις.
(α) Αποδείξτε ότι το σχήμα ελάχιστης ενέργειας για τα νανοσωματίδια του υλικού αυτού θα είναι πρισματικό μεγάλου μήκους και με άξονα κάθετο στο επίπεδο (001).
(β) Σχεδιάστε την διατομή του νανοσωματιδίου στο επίπεδο (001) που περνάει από το κέντρο του. (Υπόδειξη: εργαστείτε μόνο στην περιοχή x>0, y>0 και χρησιμοποιήστε
τη συμμετρία για να βρείτε το υπόλοιπο σχήμα.
-
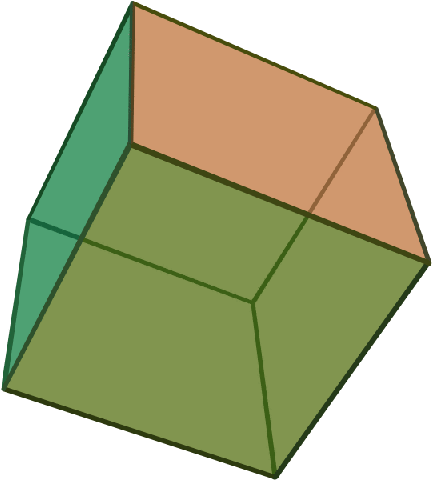
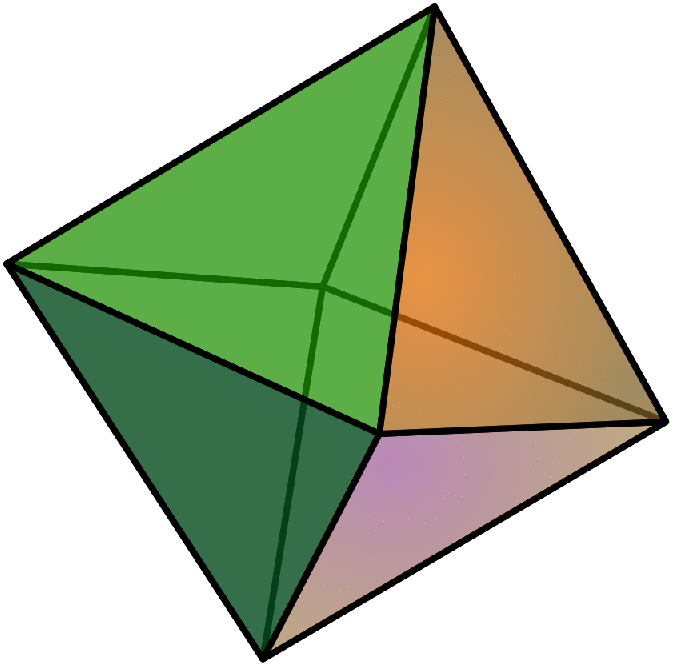
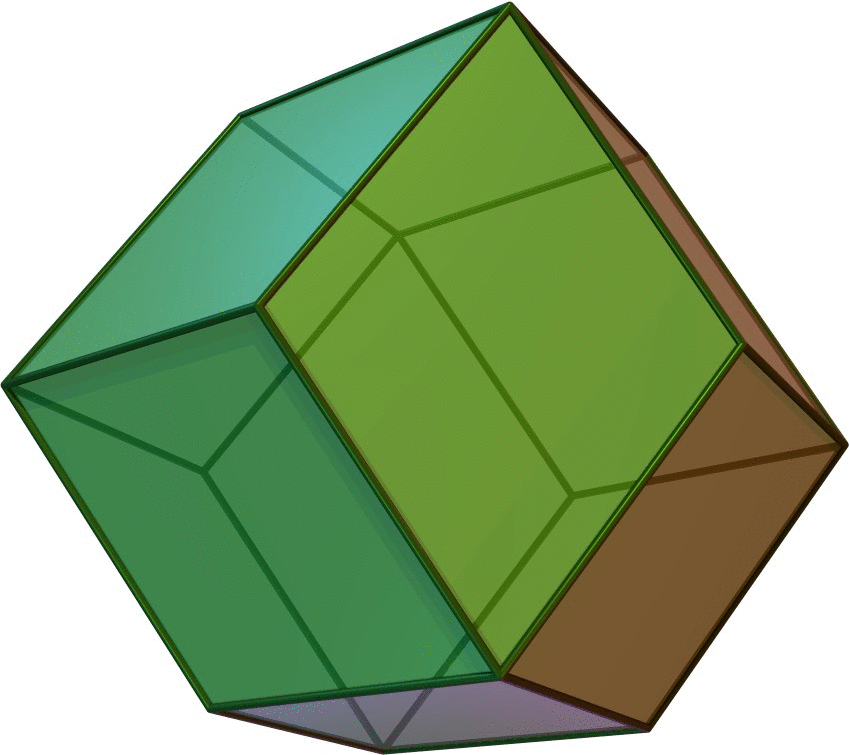
Ανάλογα με τις επιφανειακές τους τάσεις, νανοσωματίδια μετάλλων με κυβική συμμετρία μπορεί να πάρουν και μια από τις παρακάτω δομές υψηλής συμμετρίας:
 |  | 
|
| Εξάεδρο (κύβος) | Οκτάεδρο | Ρομβικό δωδεκάεδρο |
| A=6a2 | A=2√3a2 | A=8√2a2 |
| V=a3 | V=[1/3]√2a3 | V=[16/9]√3a3 |
| d=√2 a | d=a | d=[(4√2)/3]a |
(α) Εξηγείστε υπό ποιες προϋποθέσεις το σχήμα ισορροπίας ενός νανοσωματιδίου θα είναι κύβος ή οκτάεδρο ή δωδεκάεδρο.
(β) Υπολογίστε την πυκνότητα ενεργών θέσεων (θέσεις ανά μονάδα μάζας) σε κάθε ένα από τα τρία νανοσωματίδια σαν συνάρτηση της μέσης διαμέτρου, d, και παραμέτρων του υλικού αν όλα τα επιφανειακά άτομα είναι ενεργά.
(γ) Επαναλάβετε τον υπολογισμό για την περίπτωση που μόνο τα άτομα στις ακμές είναι ενεργά (όχι τα άτομα σε έδρες ή σε κορυφές). Δώστε μια πρόχειρη γραφική παράσταση.
-
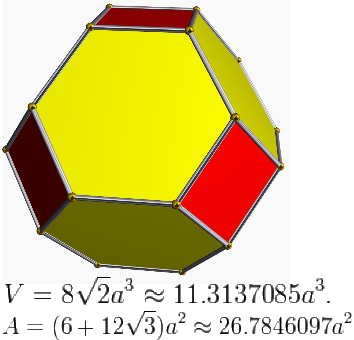 Κάποιο μέταλλο ατομικού βάρους ΑΒ και πυκνότητας ρ φτιάχνει νανοσωματίδια με σχήμα κόλουρου οκταέδρου, όπως στο διπλανό σχήμα. Το πολύεδρο αυτό έχει 14 έδρες (6 τετράγωνα και 8 εξάγωνα), 36 ακμές, όλες ίσες με α, και 24 κορυφές. Δίνονται οι τύποι για τον όγκο και το συνολικό εμβαδόν.
Oι αποστάσεις των τετράγωνων και εξαγωνικών εδρών από το κέντρο είναι
d1= √2 α και
d2= √6/2 α, αντίστοιχα.
(α) Τι μπορείτε να συνάγετε για τις επιφανειακές τάσεις των επιφανειών του μετάλλου;
(β) Υπολογίστε την ειδική επιφάνεια (συνολικό εμβαδόν δια συνολική μάζα).
(γ) Σε κάποια εφαρμογή είναι ενεργά μόνο τα άτομα των ακμών μεταξύ τετραγώνων και εξαγώνων. Υπολογίστε την συγκέντρωση ενεργών θέσεων (mol ενεργών θέσεων δια συνολική μάζα). Θεωρήστε ότι η διάμετρος του ατόμου είναι D, με D3=ΑΒ/(ρΝΑ).
Κάποιο μέταλλο ατομικού βάρους ΑΒ και πυκνότητας ρ φτιάχνει νανοσωματίδια με σχήμα κόλουρου οκταέδρου, όπως στο διπλανό σχήμα. Το πολύεδρο αυτό έχει 14 έδρες (6 τετράγωνα και 8 εξάγωνα), 36 ακμές, όλες ίσες με α, και 24 κορυφές. Δίνονται οι τύποι για τον όγκο και το συνολικό εμβαδόν.
Oι αποστάσεις των τετράγωνων και εξαγωνικών εδρών από το κέντρο είναι
d1= √2 α και
d2= √6/2 α, αντίστοιχα.
(α) Τι μπορείτε να συνάγετε για τις επιφανειακές τάσεις των επιφανειών του μετάλλου;
(β) Υπολογίστε την ειδική επιφάνεια (συνολικό εμβαδόν δια συνολική μάζα).
(γ) Σε κάποια εφαρμογή είναι ενεργά μόνο τα άτομα των ακμών μεταξύ τετραγώνων και εξαγώνων. Υπολογίστε την συγκέντρωση ενεργών θέσεων (mol ενεργών θέσεων δια συνολική μάζα). Θεωρήστε ότι η διάμετρος του ατόμου είναι D, με D3=ΑΒ/(ρΝΑ).
-
 Νανοσωματίδια Fe έχουν σχήμα εξαγωνικής ράβδου μήκους L, ενώ η πλευρά του εξαγώνου είναι a=10.2 nm. Σε κάποια εφγαρμογή κατάλυσης, είναι ενεργά μόνο τα άτομα των ακμών του νανοσωματιδίου. Η διάμετρος ενός ατόμου Fe είναι D=0.25 nm και το ατομικό βάρος του Fe είναι A=55.8 g/mol. Υπολογίστε την συγκέντρωση ενεργών θέσεων, nact σε mol/g για L=50 nm και L=200 nm.
Νανοσωματίδια Fe έχουν σχήμα εξαγωνικής ράβδου μήκους L, ενώ η πλευρά του εξαγώνου είναι a=10.2 nm. Σε κάποια εφγαρμογή κατάλυσης, είναι ενεργά μόνο τα άτομα των ακμών του νανοσωματιδίου. Η διάμετρος ενός ατόμου Fe είναι D=0.25 nm και το ατομικό βάρος του Fe είναι A=55.8 g/mol. Υπολογίστε την συγκέντρωση ενεργών θέσεων, nact σε mol/g για L=50 nm και L=200 nm.
-
 Κάποιο μέταλλο με πυκνότητα 10 g/cm3 φτιάχνει νανωσωματίδια με σχήμα κανονικού εικοσάεδρου και μέγεθος
20 nm. Τα άτομα του υλικού θεωρούνται σφαίρες με διάμετρο 0.25 nm. Υπολογίστε:
Κάποιο μέταλλο με πυκνότητα 10 g/cm3 φτιάχνει νανωσωματίδια με σχήμα κανονικού εικοσάεδρου και μέγεθος
20 nm. Τα άτομα του υλικού θεωρούνται σφαίρες με διάμετρο 0.25 nm. Υπολογίστε:
- την ειδική επιφάνεια (εμβαδόν ανά μονάδα μάζας) των νανοσωματιδίων.
- το ποσοστό των ατόμων του νανοσωματιδίου που βρίσκονται στις επιφάνειές του.
- την πυκνότητα ενεργών θέσεων (σε μmol/g) εφόσον ενεργές θέσεις θεωρούνται μόνο τα άτομα των ακμών.
- Πώς θα άλλαζαν οι απαντήσεις σας στα (α), (β), (γ) αν το μέγεθος του νανοσωματιδίου ήταν 10 nm ;
Πάρτε τύπους για τον όγκο, εμβαδόν κλπ από τον παραπάνω σύνδεσμο της Βικιπαίδειας. Ως μέγεθος του νανοσωματιδίου εννοούμε την διάμετρο της εγγεγραμένης σφαίρας, δηλαδή 2ri.
Προσρόφηση αερίων σε επιφάνειες στερεών
- Περιγράψτε τις παρακάτω υπερδομές με συμβολισμό Wood. Υπολογίστε κάθε φορά τη συγκέντρωση των προσροφημένων ατόμων ή μορίων.
- Σας δίνονται εικόνες από πειράματα LEED για τις επιφάνειες
Si(100),
Si(100) εμπλουτισμένη με C
και
Si(111).
Στις εικόνες που δεν δίνεται η περιοδικότητα της ιδανικής επιφάνειας, Θεωρήστε ότι αυτή αντιστοιχεί
στις έντονες κηλίδες. Η σκιά στο κέντρο αντιστοιχεί στο δείγμα και τους βραχίονες στηρίξεώς του. Περιγράψτε την αναδόμηση κάθε επιφάνειας στο συμβολισμό Wood.
- Στον αναλυτή του σχήματος η απόσταση δείγματος-οθόνης είναι R=4 cm. Στο δείγμα μας οι γραμμές ατόμων απέχουν κατά d=0.25nm. Βρείτε πόση πρέπει να είναι η τάση που επιταχύνει τα ηλεκτρόνια, V, ώστε τα μέγιστα περίθλασης για n=1 να πέσουν μέσα στην οθόνη, δηλαδή η απόστασή τους από το κέντρο της οθόνης να είναι μικρότερη από α=5 cm. (προσοχή: δεν ισχύει εδώ α<<R!).
Οι παρακάτω 10 ασκήσεις προέρχονται από το βιβλίο "Φυσικοχημεία" του P. Atkins.
- 1 ML (monolayer, δηλαδή θ=1.0) αζώτου προσροφάται στην επιφάνεια 1.0 g καταλύτη
Fe/Al2O3 στους 77 Κ. Θερμαίνουμε τον καταλύτη, και το εκροφώμενο άζωτο καταλαμβάνει 2.86 cm3 σε Κ.Σ. (κανονικές συνθήκες, P=1 atm και T=273 K). Κάθε προσροφημένο μόριο αζώτου καταλαμβάνει επιφάνεια 0.165 nm2. Εκτιμήστε το εμβαδόν της επιφάνειας του καταλύτη.
- Ο όγκος αερίου οξυγόνου που προσροφήθηκε σε 1 g σίλικας στους 273 Κ ήταν
0.284 cm3 όταν η πίεση κατά την προσρόφηση ήταν 142.4 Torr και
1.430 cm3 όταν η πίεση κατά την προσρόφηση ήταν 760 Torr. Οι όγκοι μετρήθηκαν σε Κ.Σ. Υπολογίστε τον όγκο (σε Κ.Σ) οξυγόνου που απαιτείται για
να καλυφθεί πλήρως η επιφάνεια στους 273 Κ.
- Η ενέργεια εκρόφησης CO σε κάποια επιφάνεια μετρήθηκε να είναι -120 kJ/mol.
Εξηγείστε αν πρόκειται για φυσιρόφηση ή χημιρόφηση. Εκτιμήστε, για Τ=400 Κ, το χρόνο που περνάει προσροφημένο το CO σε αυτήν την επιφάνεια προτού εκροφηθεί.
Υπόδειξη: t=1/k όπου k είναι ο ρυθμός εκρόφησης, k=k0exp(-Ed/RT). Θεωρήστε ότι k0=RT/NAh, όπου h έιναι η σταθερά του Plank.
- 'Aτομα οξυγόνου παραμένουν προσροφημένα σε επιφάνεια W για 0.36 sec στους 2548 Κ
και για 3.49 sec στους 2362 Κ. Εξηγείστε γιατί ο χρόνος παραμονής αυξάνεται όταν μειωθεί η θερμοκρασία. Υπολογίστε την ενέργεια εκρόφησης και την παράμετρο k0. (Υπόδειξη: δείτε την προηγούμενη άσκηση).
- Υπολογίστε πόσο περίπου χρόνο θα παραμείνει προσροφημένο ένα άτομο σε μια επιφάνεια στους 400 Κ, αν η ενέργεια εκρόφησης είναι (α) 15 kJ/mol ή (β) 150 kJ/mol. Θεωρήστε ότι k0=RT/NAh. Επαναλάβετε την άσκηση για Τ=1000 Κ.
- Προσρόφηση κάποιου αερίου σε κάποια επιφάνεια περιγράφεται από τον τύπο του Langmuir με Κ=0.85 (kPa)-1. Υπολογίστε την πίεση για την οποία η συγκέντρωση θ
είναι (α) 0.15 και (β) 0.95.
- Κάποιο στερεό προσροφά 0.44 mg CO σε πίεση 36.0 kPa και θερμοκρασία 300 Κ, ενώ
σε πίεση 4.0 kPa και θερμοκρασία 300 Κ προσροφά 0.21 mg. Γνωρίζουμε ότι η προσρόφηση περιγράφεται από τον τύπο του Langmuir. Υπολογίστε την επιφανειακή συγκέντρωση, θ, για τις δυο παραπάνω τιμές της πίεσης.
- Υποθέστε ότι η προσρόφηση του όζοντος σε κάποια επιφάνεια περιγράφεται από τη θεωρία του Langmuir. Εξηγείστε τι πειράματα θα εκτελούσατε για να εξακριβώσετε αν η προσρόφηση γίνεται (α) μοριακά ή (β) με διάσπαση σε Ο+Ο2 ή (γ) με διάσπαση σε Ο+Ο+Ο.
- Εκτελούμε πείραμα προσρόφησης αζώτου σε κάρβουνο. Στους 190 Κ και υπό πίεση 490 kPa, απαιτούνται 0.921 cm3 αζώτου (μετρημένα σε Κ.Σ) ανά γραμμάριο κάρβουνου. Στους 250 Κ, για να επιτύχουμε προσρόφηση ίσης ποσότητας αζώτου απαιτείται
πίεση 3.2 MPa. Υπολογίστε την ενθαλπία προσρόφησης του αζώτου στο κάρβουνο.
- Τα παρακάτω δεδομένα αφορούν χημιρόφηση υδρογόνου σε ρινίσματα χαλκού στους 298 Κ. P είναι η πίεση του αερίου υδρογόνου, και V o όγκος του προσροφημένου αερίου, μετρημένος σε Κ.Σ. Επιβεβαιώστε ότι περιγράφονται από τον τύπο του Langmuir.
Υπολογίστε τη σταθερά K και τον όγκο προσροφημένου υδρογόνου ο οποίος αντιστοιχεί σε πλήρη κάλυψη.
| P (Torr) | 0.19 | 0.97 | 1.9 | 4.1 | 7.5 | 12. |
| V (cm3) | 0.04 | 0.16 | 0.22 | 0.32 | 0.41 | 0.47 |
-
Τα παρακάτω δεδομένα αφορούν προσρόφηση Η_2 σε ρινίσματα Cu στους 298 K. Δίνεται η πίεση του κάθε πειράματος και ο όγκος που καταλαμβάνει κάθε φορά το προσροφημένο Η_2 σε κανονικές συνθήκες. Επιβεβαιώστε ότι ακολουθούν την ισόθερμη του Langmuir, και βρείτε τον όγκο του Η2 που απαιτείται για πλήρη κάλυψη
(θ = 1).
| P/Pa | 25 | 129 | 253 | 540 | 1000 | 1593 |
| V/cm3 | 0.042 | 0.163 | 0.221 | 0.321 | 0.411 | 0.471 |
- Μια επιφάνεια μετάλλου είναι σε ισορροπία με αέρια N2 και H2. Δεν
παρατηρείται διάσπαση του μορίων αζώτου. Αντίθετα, το υδρογόνο διασπάται
ακαριαία πάνω στο μέταλλο, έτσι ώστε πρακτικά να υπάρχουν μόνο άτομα υδρογόνου
στην επιφάνεια. Τα προσροφημένα μόρια δεν αντιδρούν μεταξύ τους.
α) Υπολογίστε πώς εξαρτώνται οι επιφανειακές συγκεντρώσεις από τις μερικές
πιέσεις.
β) Υπολογίστε τις επιφανειακές συγκεντρώσεις σε κανονικές συνθήκες, και για 10
φορές περισσότερο αέριο άζωτο από ότι υδρογόνο. Δίνονται οι ενέργειες
προσρόφησης ΔHADN2=-20 και ΔHADΗ=-60
-
Υποθέστε ότι σας δίνουν ένα κομμάτι από κάποιο νέο μεταλλικό κράμα και
σας ζητούν να εξετάσετε αν είναι κατάλληλο για αποθήκευση υδρογόνου. Το
ζητούμενο δηλαδή είναι να προσροφάται υδρογόνο στο μέταλλο, το οποίο μετά θα
ανακτάται με θέρμανση. Περιγράψτε τι πειράματα θα κάνατε ώστε να διαπιστώσετε:
(α) αν προσροφώνται άτομα ή μόρια υδρογόνου.
(β) πόσο ισχυρός είναι ο δεσμός μεταξύ του υδρογόνου και του μετάλλου.
(γ) πώς ακριβώς προσροφούνται τα υδρογόνα στο μέταλλο (περιοδικότητα και τι
είδους δεσμό κάνουν με τα άτομα του μετάλλου).
(δ) πόση είναι η επιφανειακή συγκέντρωση του υδρογόνου για δεδομένη
πίεση και θερμοκρασία του αερίου.
Σε κάθε περίπτωση, δώστε κι ένα σύντομο παράδειγμα.
-
Το Ti σχηματίζει κρύσταλλο δομής hcp με πλεγματικές
σταθερές a=2.95 Å και c=4.66 Å. Η ενέργεια συνοχής του στερεόυ
Ti είναι 4.9 eV.
(α) Σχεδιάστε την κάτοψη της επιφάνειας Ti(001), δείχνοντας τα
επιφανειακά άτομα και τα άτομα του δευτέρου επιπέδου. Βρείτε τα διανύσματα
βάσης για την επιφάνεια, και δώστε τις συνιστώσες τους σε σύστημα
αξόνων της επιλογής σας.
(β) Υπολογίστε την επιφανειακή πυκνότητα ατόμων, και τη μάζα του
υδρογόνου που απαιτείται για να καλυφθεί πλήρως 100 cm2
επιφάνειας, αν κάθε άτομο Ti καλύπτεται από ένα άτομο
H.
(γ) Εκτιμήστε πόσο χρόνο θα πάρει για να καλυθφεί η παραπάνω
επιφάνεια με υδρογόνο, αν το αέριο υδρογόνο είναι σε κανονικές συνθήκες.
(δ) Εκτιμήστε την επιφανειακή τάση της Ti(001).
-
Πειραματιζόμενοι με την Ni(100), βρήκαμε ότι ο C φτιάχνει μια υπερδομή c(6x2), με τα άτομα C να είναι σε θέσεις on top (δηλαδή συνδέονται με ένα άτομο Ni) ή bridge (δηλαδή συνδέονται με δυο άτομα Ni). Το ποσοστό επικάλυψης είναι θ=0.8.
(α) Περιγράψτε λεπτομερώς τα πειράματα που έγιναν για να πάρουμε τις παραπάνω πληροφορίες.
(β) Σχεδιάστε μια πιθανή δομή των ατόμων του C πάνω στην Ni(100) (το Ni έχει δομή fcc).
-
Το τσιμέντο είναι εξαιρετικά πορώδες υλικό. Ένα κομμάτι τσιμέντου μάζας 100 g αφήνεται να αλληλεπιδράσει με άερα με υγρασία υπό σταθερή θερμοκρασία. Στη συνέχεια μετριέται ο όγκος υδρατμών (V) που προσκολλήθηκε στην επιφάνεια σαν συνάρτηση της σχετικής υγρασίας (z=P/P_0). H γραφική παράσταση του (1/V) * (z/(1-z)) σαν συνάρτηση του z προέκυψε ευθεία με κλίση 24.2 l-1, η οποία τέμνει τον άξονα y στο σημείο 0.33 l-1.
Μπορείτε να υπολογίσετε από αυτά τα δεδομένα την ειδική επιφάνεια (σε m2/g) του συγκεκριμένου τσιμέντου? (η ειδική επιφάνεια ορίζεται ως το πηλίκο της επιφάνειας ενός υλικού δια τη μάζα του.) Θεωρήστε για απλότητα ότι το μόριο του νερού είναι σφαίρα ακτίνας 2 A.
-
 H διπλανή εικόνα δείχνει άτομα της επιφάνειας Pt(111). Άτομα H προσροφώνται στην επιφάνεια και σχηματίζουν περιοδική υπερδομή.
Σημειώστε τις θέσεις των ατόμων H και τα διανύσματα βάσης ώστε η υπερδομή να έχει
H διπλανή εικόνα δείχνει άτομα της επιφάνειας Pt(111). Άτομα H προσροφώνται στην επιφάνεια και σχηματίζουν περιοδική υπερδομή.
Σημειώστε τις θέσεις των ατόμων H και τα διανύσματα βάσης ώστε η υπερδομή να έχει
- θ = 0.25.
- θ = 0.7.
- περιοδικότητα $(6x8)$.
- περιοδικότητα (√3x√3) R30o.
Σημειώστε την περιοδικότητα στα (α) και (β) και βρείτε το θ στα (γ) και (δ).
- Σε πείραμα προσρόφησης O σε νανοσωματίδια W, παρατηρήθηκε ότι μια συγκριμένη σταθερή ποσότητα Ο εκροφάται σε 27 λεπτά στους 1856 Κ και σε μόλις 2 λεπτά στους 1978 Κ. Σε πόση ώρα θα εκροφηθεί η ίδια ποσότητα (α) στους 298 Κ
και (β) στους 3000 Κ;
- (α) Υπολογίστε το χρόνο που απαιτείται κατά μέσο όρο για να σχηματιστεί 1 ML CO στην επιφάνεια Pt(111) στους 200Κ υπό πίεση 1 Torr. Ο Pt έχει δομή fcc με πλεγματική σταθερά a=0.392 nm.
(β) Υπολογίστε πόσο περίπου χρόνο θα παραμείνει προσροφημένο ένα μόριο CO στην παραπάνω επιφάνεια και στις συνθήκες αυτές. Δίνεται ότι η ενέργεια εκρόφησης είναι 100 kJ/mol. Θεωρήστε ότι k0=RT/NAh. kB = 1.38x10-23 J K-1.
-
Για τις παρακάτω υπερδομές (από την εξαιρετική σελίδα του Roger M. Nix, An Introduction to Surface Chemistry): (α) Περιγράψτε την περιοδικότητα με συμβολισμό Wood και (β) βρείτε το ποσοστό επικάλυψης, θ.
-
Μια αρχικά καθαρή επιφάνεια Ni(100) έρχεται σε ΚΣ σε επαφή με αέριο πίεσης P που περιέχει 100% CO. To Ni έχι δομή fcc με πλεγματική σταθερά a = 0.35 nm. H προσρόφηση του CO έχει 100% προσκόλληση (δηλαδή όλα τα μόρια που χτυπάν την επιφάνεια προσκολλώνται σε αυτήν). Η εκρόφηση του CO έχει ρυθμό k2 = k0 e- E/kT, με k0 = 1013 s-1 και Ε = 0.5 eV.
- Δείξτε ότι το ποσοστό επικάλυψης, θ, υπακούει την διαφορική εξίσωση dθ/dt = k1 P(1-θ)-k2θ. Πόσο είναι το k1;
- Λύστε την εξίσωση και σχεδιάστε πρόχειρα το θ σαν συνάρτηση του χρόνου. Μετά από πόσο χρόνο περίπου το θ γίνεται σταθερό;
Υπόδειξη: Έστω Ν προσροφημένα μόρια στην επιφάνεια και Νt ο μέγιστος αριθμός προσροφημένων μορίων. Όταν Ν << Νt θα είναι dN/dt = S Z A, όπου S η πιθανότητα προσκόλλησης, Ζ ο ρυθμός Hertz-Knudsen και Α το εμβαδόν της επιφάνειας.
-
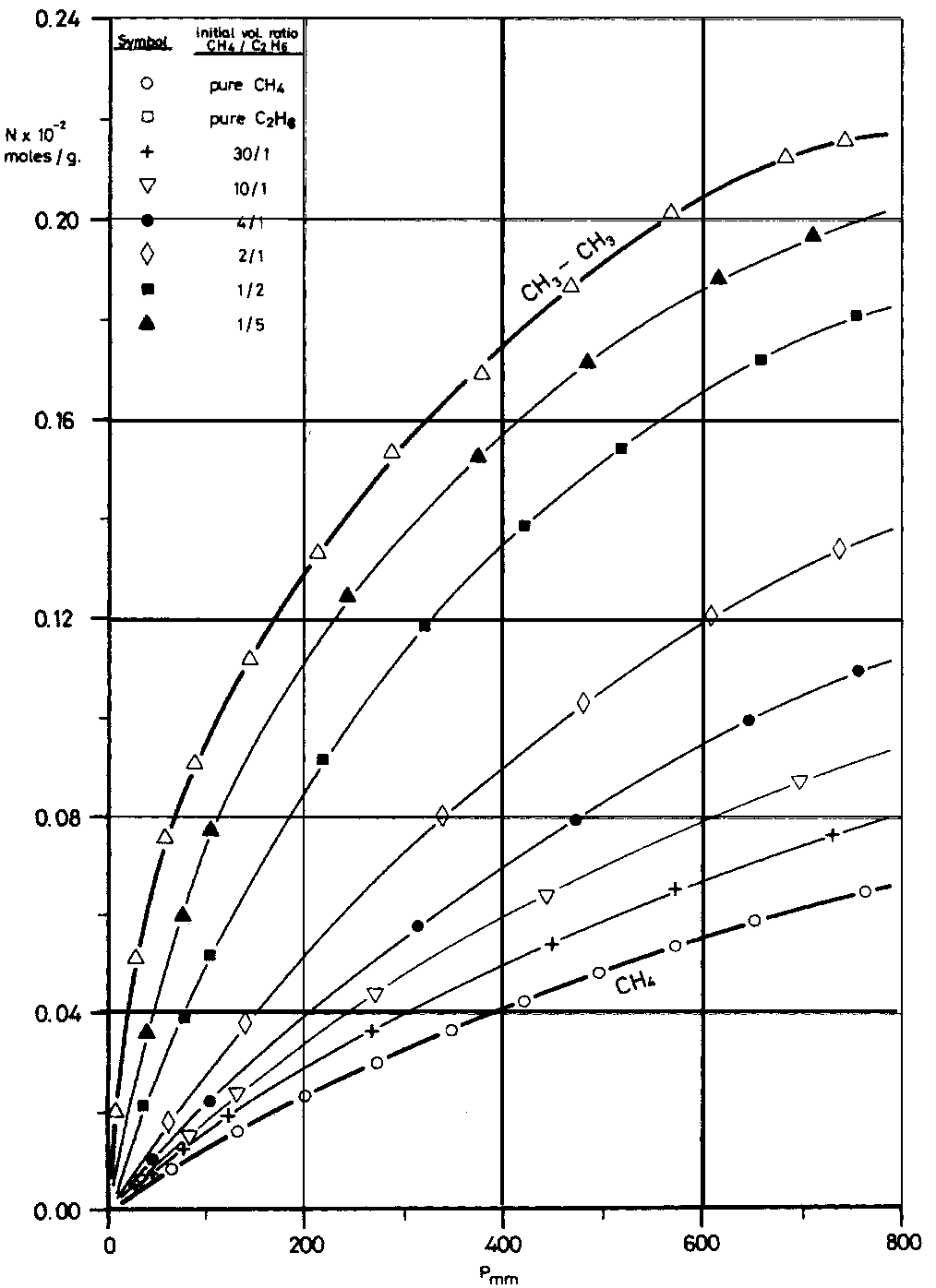 Το σχήμα δείχνει καμπύλες μοριακής προσρόφησης αιθανίου, μεθανίου και μιγμάτων τους σε ενεργό άνθρακα. Θεωρήστε ότι το φαινόμενο περιγράφεται με την εξίσωση του Langmuir, N/N∞=KP/(1+KP), όπου
N∞ η οριακή τιμή του N για άπειρη πίεση.
Το σχήμα δείχνει καμπύλες μοριακής προσρόφησης αιθανίου, μεθανίου και μιγμάτων τους σε ενεργό άνθρακα. Θεωρήστε ότι το φαινόμενο περιγράφεται με την εξίσωση του Langmuir, N/N∞=KP/(1+KP), όπου
N∞ η οριακή τιμή του N για άπειρη πίεση.
- Βρείτε τις συντεταγμένες (P, N) για δυο σημεία της καμπύλης του αιθανίου.
- Λύστε την εξίσωση Langmuir ως προς K. Αντικαταστήστε τις τιμές των παραπάνω σημείων. Βρείτε το N∞ για το αιθάνιο.
- Επαναλάβετε τα (α) και (β) για το μεθάνιο.
- Επαναλάβετε τα (α) και (β) για το μίγμα CH4/CH3CH3=2/1.
- Συγκρίνετε τα αποτελέσματα για το N∞ στα τρία αέρια. Τι συμπεράσματα βγάζετε;
Κατάλυση
-
Εκτελούμε τα παρακάτω πειράματα προσρόφησης στην ίδια επιφάνεια και στις ίδιες συνθήκες (P,T). Στην αρχή κάθε πειράματος η επιφάνεια είναι καθαρή.
(α) Αέριο H2, με μερική πίεση P1, προσροφάται σε ποσοστό επικάλυψης θ1.
(β) Αέριο Cl2, με μερική πίεση P2, προσροφάται σε ποσοστό επικάλυψης θ2.
(γ) Αέριο HCl, με μερική πίεση P3, προσροφάται σε ποσοστό επικάλυψης θ3.
(δ) Μίγμα των αερίων H2, Cl2 και HCl με μερικές πιέσεις P1, P2, και P3 αντίστοιχα, προσροφάται στην ίδια επιφάνεια. Τα H2, Cl2 και HCl δεν αντιδρούν στην αέρια φάση. Το ποσοστό επικάλυψης του H2 είναι θ1'. Υπολογίστε το θ1' σαν συνάρτηση των θ1, θ2,θ3, P1, P2,P3 σε δυο περιπτώσεις:
(1) Όταν τα H2, Cl2 και HCl δεν αντιδρούν μεταξύ τους, και
(2) Όταν H2*+Cl2* ↔ 2HCl με σταθερά ισορροπίας K=1.
- Χρησιμοποιώντας καταλύτη Pt, το μεθυλοκυκλοεξάνιο (CH3-C6H11, Μ) μετατρέπεται σε τολουόλιο
(CH3-C6H5, Τ) απελευθερώνοντας υδρογόνο. Τα στάδια της αντίδρασης είναι
- Προσρόφηση του Μ.
- Μετατροπή του προσροφημένου Μ σε προσροφημένο Τ και αέριο H2.
- Εκρόφηση του προσροφημένου Τ.
Θεωρήστε ότι η ταχύτητα της αντίδρασης καθορίζεται από το τρίτο βήμα (RDS), ενώ τα άλλα δυο βρίσκονται σε χημική ισορροπία. Υποθέτουμε ότι το Μ έχει πολύ ασθενή προσρόφηση ώστε θM=0.
- Γράψτε τις αντιδράσεις (1)-(3).
- Βρείτε πώς εξαρτώνται οι καλύψεις θT, θ* από τις μερικές πιέσεις των Μ, Τ, Η2.
- Βρείτε πώς εξαρτάται η ταχύτητα της αντίδρασης (3) από τις μερικές πιέσειςτων Μ, Τ, Η2 .
-
Στις κυψέλες καυσίμου χρησιμοποιείται καταλύτης Pt στον οποίο το υδρογόνο προσροφάται με διάσπαση, και εν συνεχεία τα άτομα υδρογόνου χρησιμοποιούνται για την παραγωγή ενέργειας. Το αέριο υδρογόνο όμως περιέχει και ίχνη CO, το οποίο επίσης προσροφάται στην επιφάνεια. Καθώς μάλιστα έχει μεγαλύτερη ενέργεια εκρόφησης (EdCO=100 kJ/mol
ενώ EdΗ=80 kJ/mol), καταλαμβάνει τις περισότερες θέσεις στην επιφάνεια, μη αφήνοντας χώρο για το υδρογόνο.
Υπολογίστε τις συγκεντρώσεις θH, θCO και θ* για P=1 bar και θερμοκρασία 80oC, όταν η
περιεκτικότητα του υδρογόνου σε CO είναι (α) 1 ppm ή (β) 100 ppm. Δίνεται ότι η επιφάνεια του καταλύτη είναι Pt(111) και ο Pt έχει δομή fcc με α=0.392 nm, και οι σταθερές της φταχύτητας αντιδράσεων
(ν=1013 sec-1):
| H2+2*↔2H* |
k1+=2PAat/√(2πmH2kBT) |
k1-=v exp(-EdΗ/RT) |
| CO+*↔CO* |
k2+=PAat/√(2πmCOkBT) |
k2-=v exp(-EdCO/RT) |
Υπόδειξη: Α+Β↔C έχει ρυθμό παραγωγής του C r=k+[A][B]-k-[C] όπου [Χ] η συγκέντρωση του X και r η παράγωγος του [C] ως προς τον χρόνο.
- Η αντίδραση μεθανοποίησης μετατρέπει μίγμα CO και H2 σε αναλογία 1:3 (synthesis gas)
πρώτα σε φορμαλδεΰδη (CH2Ο) και εν συνεχεία,
με αφαίρεση του Ο και προσθήκη H2, σε μεθάνιο. Το προσροφημένο Ο που μένει στην επιφάνεια αντιδράει με προσροφημένο υδρογόνο και δημιουργεί υδρατμό. Η συνολική αντίδραση είναι CO+3H2↔CH4+H2O και γίνεται σε καταλύτη Ni.
(α) Γράψτε τις στοιχειώδεις αντιδράσεις που περιγράφουν τη διεργασία. Θεωρήστε ότι το υδρογόνο προσροφάται με διάσπαση.
(β) Βρείτε πως εξαρτάται η ταχύτητα της αντίδρασης από τις μερικές πιέσεις, θεωρώντας ότι το CH2 έχει τη μεγαλύτερη ενέργεια εκρόφησης, και επομένως θ*=1-θCH2. Θεωρήστε ότι όλες οι αντιδράσεις είναι σε ισορροπία εκτός από μια, η οποία καθορίζει την ταχύτητα (RDS). Πάρτε δυο περιπτώσεις: πρώτα ότι RDS είναι η αντίδραση μεταξύ CO* και H* και κατόπιν ότι RDS είναι η αντίδραση διάσπασης της φορμαλδεΰδης σε CH2 και O.
- Το άεριο άζωτο προσροφάται σε καταλύτη Ru, και εν συνεχεία διασπάται σε άτομα αζώτου. Οι αντιδράσεις και οι τύποι που δίνουν τις σταθερές ταχύτητας αντίδρασης είναι:
| N2+*↔N2* |
k1+=P/ns√(2πmN2kBT) |
k1-=v1 exp(-Ed/RT) |
| N2*+*↔2N* |
k2+=v2 exp(-Ea/RT) |
k2-=v2' exp(-Ea'/RT) |
(α) Δικαιολογήστε τη μορφή που έχουν οι τύποι για τις σταθερές ταχύτητας.
(β) Υπολογίστε τη συγκέντρωση ατόμων αζώτου και κενών θέσεων σαν συνάρτηση της πίεσης του αζώτου και της θερμοκρασίας.
Θεωρήστε ότι έχουμε θερμοδυναμική ισορροπία. Πάρτε v1=v2=v2'=RT/NAh, όπου h έιναι η σταθερά του Plank. Για να βρείτε το ns, θεωρήστε την Ru(001) και ότι το Ru έχει δομή hcp με α=0.271nm. Πάρτε τις ενέργειες που μπαίνουν στους τύπους από το θεωρητικό υπολογισμό της εικόνας.
Θεωρήστε δυο περιπτώσεις: Πρώτα προσρόφηση σε άτομα Ru που βρίσκονται σε επίπεδο (terrace) και μετά προσρόφηση σε άτομα Ru που βρίσκονται σε σκαλοπάτι (step).
- Το προηγούμενο πρόβλημα μπορεί να λυθεί και χωρίς να υποθέσουμε χημική ισορροπία. Μπορούμε δηλαδή να εξάγουμε πώς εξαρτώνται οι συγκεντρώσεις από το χρόνο, και όχι απλά τις αυμπτωτικές τιμές τους μετά από άπειρο χρόνο.
(α) Δείξτε πρώτα ότι απαιτείται λύση συστήματος 4 διαφορικών εξισώσεων με 4 άγνωστες συναρτήσεις:
dpN2/dt=-k1+ pN2θ* + k1- θN2
dθ*/dt = -k1+ pN2θ* +
k1- θN2 -
k2+ θN2θ* +
k2- θN2
dθN2/dt =
k1+ pN2θ* -
k1- θN2 -
k2+ θN2θ* +
k2- θN2
dθN/dt = -2 k2- θN2 + 2 k2+ θN2 θ*
Οι αρχικές συθήκες είναι ότι για t=0 έχουμε pN2=1, θ*=1 και θN2=θN=0.
(β) Δείξτε ότι στη χημική ισορροπία, όπου οι συγκεντρώσεις δεν εξαρτώνται από το χρόνο, οι εξισώσεις δίνουν τα αποτελέσματα της προηγούμενης άσκησης.
(γ) Δείξτε ότι σε κάθε χρονική στιγμή θ*+θN2+θN=1.
(δ) Μας ενδιαφέρουν πιέσεις της τάξεως των 100 bar, και θερμοκρασίες μερικών εκατοναδων βαθμών Κελσίου. Δικαιολογήστε, με βάση τους τύπους της προηγούμενης άσκησης και το σχήμα ότι σε αυτές τις συνθήκες η k1+
είναι κατά πολύ μεγαλύτερη από τις άλλες, και ότι οι k2+ και k2- θα είναι περίπου ίσες.
(ε) Ακόμα και με την προσέγγιση αυτή, όμως, προκύπτει μή γραμμικό σύστημα το οποίο δεν λύνεται ακριβώς. Πάντως λύνεται πολύ έυκολα αριθμητικά. Αν είστε δυνατοί στις διαφορικές εξισώσεις και στην υπολογιστική επιστήμη υλικών, δοκιμάστε το!
- Ο λευκόχρυσος χρησιμοποιείται ως καταλύτης για την καύση του υδρογόνου (στις αρχές του 19ου αιώνα φτιάχτηκαν οι πρώτοι αναπτήρες οι οποίοι λειτουργόυσαν με αυτή την αρχή!). Η αντίδραση ξεκινάει με την προσρόφηση του οξυγόνου και του υδρογόνου στην επιφάνεια. Και οι δυο προσροφήσεις γίνονται με απευθείας διάσπαση. Στη συνέχεια, τα O* και H* ενώνονται για να φτιάξουν υδροξύλιο, το οποίο εν συνεχεία γίνεται νερό με προσθήκη ενός ακόμα υδρογόνου.
(α) Δικαιολογήστε ότι η ανιδραση O*+H*↔OH*+* είναι πολύ πιο αργή από τις άλλες και επομένως θα καθορίζει την ταχύτητα (RDS).
(γ) Δείξτε ότι η ταχύτητα της αντίδρασης είναι ανάλογη του
(PH2PO2)0.5θ*2.
(δ) Υπολογίστε το θ* θεωρώντας ότι οι το οξυγόνο έχει πολύ μεγαλύτερο ποσοστό επικάλυψης από ότι το υδρογόνο, ενώ το νερό έχει αμελητέο θ.
(ε) Θεωρήστε ότι PH2O=0.1PH2, και ότι PH2+PO2=1. Βρείτε την τιμή της πίεσης του υδρογόνου στην οποία η ταχύτητα της αντίδρασης γίνεται μέγιστη.
- Η σύνθεση της αμμωνίας με τη μέθοδο Haber-Bosch έχει τα ακόλουθα ενδιάμεσα στάδια (δίνονται και οι σχετικές εξισώσεις):
| N2+*↔N2* | θN2=Κ1PN2θ* | (1) |
| N2*+*↔2N* (RDS) | r=k θN2θ* - (k/K2) θN2 | (2) |
| N*+H*↔NH*+* | θN=θNHθ*/(K3θH) | (3) |
| NH*+H*↔NH2*+* | θNH=θNH2θ*/(K4θH) | (4) |
| NH2*+H*↔NH3*+* | θNH2=θNH3θ*/(K5θH) | (5) |
| NH3*↔NH3+* | θNH3=(1/K6)PNH3θ* | (6) |
| H2+2*↔2H* | θH=√(Κ7 PH2) θ* | (7) |
| Αριθμοί επιφανειακών θέσεων: | θN2+θN+θNH+θNH2+θNH3+θH+θ*=1 |
(8) |
Εμπειρικά, χρησιμοποιείται ο τύπος
r=a (KGPN2-PNH32/PH23)/
(1+γPNH3/PH2w)2.
Βρείτε τη σταθερά w. Πώς σχετίζονται οι άλλες σταθερές στον εμπειρικό τύπο με τις σταθερές των παραπάνω επιμέρους αντιδράσεων;
-
Επιφάνεια Ni(100) είναι σε ισορροπία με αέριo που περιέχει CO, CO2 και κάποιο αδρανές αέριο. Πάνω στην επιφάνεια του καταλύτη, το CO μετατρέπεται σε CO2 σύμφωνα με το μηχανισμό Eley-Rideal:
| CO+* ↔ CO* | (1) |
| CO+ CO* ↔ CO$_2$ + C* | (2) |
(α) Αγνοήστε προς το παρόν τη (2). Ο ρυθμός μεταβολής του ποσοστού επικάλυψης του CO είναι
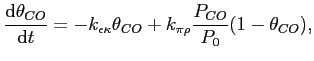 με θCO(0)=0.
Yπολογίστε το θCO σα συνάρτηση του χρόνου. Βρείτε το όριο για t→∞ και σχολιάστε το.
(β) Υπολογίστε, στην ταυτόχρονη ισορροπία των (1) και (2), τα ποσοστά επικάλυψης σαν συνάρτηση των μερικών πιέσεων και των σταθερών ισορροπίας.
με θCO(0)=0.
Yπολογίστε το θCO σα συνάρτηση του χρόνου. Βρείτε το όριο για t→∞ και σχολιάστε το.
(β) Υπολογίστε, στην ταυτόχρονη ισορροπία των (1) και (2), τα ποσοστά επικάλυψης σαν συνάρτηση των μερικών πιέσεων και των σταθερών ισορροπίας.
-
To υδρογόνο προσροφάται με διάσπαση στην Pt(111). Βρείτε πώς εξαρτάται το ποσοστό επικάλυψης υδρογόνου από την μερική πίεση του αερίου υδρογόνου:
(α) όταν η προσρόφηση γίνεται απευθείας, δηλαδή H2+2* ↔ 2H* και
(β) όταν η προσρόφηση γίνεται σε δυο στάδια, δηλαδή H2+* ↔ H2* και στη συνέχεια H2*+* ↔ 2H*.
(γ) Βρείτε τη συνθήκη ώστε οι δυο παραπάνω προσεγγίσεις να δίνουν ίδιο ποσοστό επικάλυψης.
-
Στις κυψέλες καυσίμου χρησιμοποιείται καταλύτης Pt στον οποίο το υδρογόνο προσροφάται με διάσπαση, και εν συνεχεία τα άτομα υδρογόνου χρησιμοποιούνται για την παραγωγή ενέργειας. Το αέριο υδρογόνο συνήθως περιέχει και ίχνη CO, το οποίο επίσης προσροφάται στην επιφάνεια, και μάλιστα με μεγαλύτερη ενέργεια εκρόφησης: EdCO=100 kJ/mol ενώ EdH=80 kJ/mol. Αυτό έχει σαν αποτέλεσμα να μην υπάρχουν αρκετές ελεύθερες θέσεις για να προσροφηθεί το υδρογόνο.
Εξηγήστε το φαινόμενο. Κατ' αρχάς υπολογίστε τις συγκεντρώσεις θH και θCO για P=1 bar και θερμοκρασία 80 βαθμούς C, όταν η περιεκτικότητα του υδρογόνου σε CO είναι
(α) 1 ppm ή (β) 10 ppm ή (γ) 100 ppm.
Θεωρήστε ότι ο καταλύτης είναι επιφάνεια Pt(111). O Pt έχει δομή fcc με a=0.392 nm. Η σταθερά ταχύτητας προσρόφησης περιέχει τον τύπο του Knudsen, ενώ η σταθερά ταχύτητας εκρόφησης δίνεται από τη σχέση του Arrhenius, k=ν exp(-E/RT) με ν=1013 s-1.
-
Στους καταλύτες των αυτοκινήτων γίνεται αντίδραση ταυτόχρονης αναγωγής του ΝO και οξείδωσης του CO:
Το βήμα που καθορίζει το ρυθμό είναι το
Τα άλλα βήματα είναι τόσο γρήγορα που μπορούν να θεωρηθούν ότι είναι πάντα σε ισορροπία. Αυτά είναι:
3. Προσρόφηση του NO.
4. Προσρόφηση του CO.
5. Οξείδωση του προσροφημένου CO σε αέριο CO2 (δεν υπάρχει προσροφημένο CO2).
6. Αναγωγή του προσροφημένου Ν σε αέριο Ν2 (δεν υπάρχει προσροφημένο Ν2).
(α) Γράψτε τις αντιδράσεις που αντιστοιχούν στα παραπάνω βήματα. Αποδείξτε με βάση αυτές ότι η ταχύτητα της αντίδρασης (2)είναι ανάλογη του θ*2.
(β) Εκφράστε τη σταθερά χημικής ισορροπίας της αντίδρασης (1) σαν συνάρτηση των σταθερών ισορροπίας των επιμέρους αντιδράσεων (2-6).
-
Θεωρήστε την πρότυπη αντίδραση Langmuir Hinshelwood σε τρία βήματα:
Οι δυο πρώτες αντιδράσεις είναι σε ισορροπία με σταθερές ισορροπίας K1 και K2, ενώ η τρίτη είναι μονόδρομη. Η συγκέντρωση του C είναι αμελητέα, ώστε οι συγκεντρώσεις των αερίων Α και Β να ικανοποιούν την
pA + pB = 1.
(α) Αποδείξτε ότι εαν K1 = K2, τότε η ταχύτητα της αντίδρασης (3) γίνεται μέγιστη όταν
pA = pB = 1/2.
(β) Βρείτε για ποιές τιμές των pA, pB η ταχύτητα γίνεται μέγιστη στην γενική περίπτωση όπου
K1 ≠ K2.
-
Ο μηχανισμός Michaelis-Menten περιγράφει τη στοιχειώδη αντίδραση R→P σε ένζυμο (*) ως εξής:
(α) R+*↔R* και
(β) R*→P+*.
Η πρώτη αντίδραση είναι σε ισορροπία, ενώ η δεύτερη καθορίζει την ταχύτητα και είναι μονόδρομη προς τα δεξιά.
1) Αποδείξτε ότι η ταχύτητα της αντίδρασης δίνεται από την r=apR/(b+pR), όπου pR η συγκέντρωση του R και a,b σταθερές. Πώς σχετίζονται οι a,b με τις σταθερές ταχύτητας αντιδράσεων των αντιδράσεων (α) και (β);
2) Έστω ότι κάποιος προτείνει έναν παρόμοιο μηχανισμό αλλά με τρία βήματα:
(α) R+*↔R*
(β) R*↔Χ* και
(γ) Χ*→P+*.
Υπολογίστε το r σαν συνάρτηση του pR και σταθερών.
Μπορείτε να αποφανθείτε ποιος από τους δυο μηχανισμούς είναι ο σωστός από μετρήσεις του r σαν συνάρτηση του pR; Αν ναι, πώς; Αν όχι, τι άλλη μέτρηση χρειάζεται;
-
Η αντίδραση CO + H2O → CO2 + H2 λέγεται στα αγγλικά water gas shift reaction. Γίνεται σε καταλύτη σε 5 στάδια:
- Προσρόφηση με διάσπαση Η2Ο: H2O + 2* ↔ H* + OH*
- Προσρόφηση χωρίς διάσπαση του CO.
- Δημιουργία καρβοξυλίου: CO*+OH* → COOH* + *.
- Διάσπαση του COOH* σε αέριο CO2 και προσροφημένο H*.
- ---.
(α) Γράψτε τις εξισώσεις των αντιδράσεων (2), (4) και (5).
(β) Γράψτε μια έκφραση για την ταχύτητα της (4) σαν συνάρτηση πιέσεων και ποσοστών επικάλυψης. Το ίδιο για την (3). Θεωρήστε ότι είναι μονόδρομες προς τα δεξιά.
-
Ο μηχανισμός Michaelis-Menten περιγράφει τη στοιχειώδη αντίδραση R→P σε ένζυμο (*) ως εξής:
(α) R+*↔R* και
(β) R*→P+*.
Η πρώτη αντίδραση είναι σε ισορροπία, ενώ η δεύτερη καθορίζει την ταχύτητα και είναι μονόδρομη προς τα δεξιά. Δώστε τη γραφική της παράσταση της ταχύτητας αντίδρασης σαν συνάρτηση της συγκέντρωσης του R. Τι πληροφορίες μπορούμε να αντλήσουμε από μια τέτοια γραφική παράσταση;
-
Το οξιράνιο (CH2ΟCH2) παράγεται βιομηχανικά από oξείδωση αιθενίου (CH2CH2):
CH2CH2+1/2O2 → CH2ΟCH2
Η αντίδραση γίνεται καταλυτικά με τον μηχανισμό Eley-Rideal σε δυο στάδια:
(α) προσρόφηση του Ο2 με απευθείας διάσπαση σε προσροφημένο ατομικό οξυγόνο (Ο*)
(β) Αντίδραση του Ο* με αέριο αιθένιο και απευθείας δημιουργία αερίου οξιρανίου.
1) Γράψτε τις επιμέρους αντιδράσεις για τα βήματα (α) και (β).
2) Αποδείξτε ότι αν το βήμα που καθορίζει τον ρυθμό είναι το (β) τότε ο ρυθμός παραγωγής οξιρανίου εξαρτάται από την συγκέντρωση του O2 με συνάρτηση της μορφής f(x) = a√ x /(1+b√ x ) (a,b σταθερές).
3) Αποδείξτε ότι αν το βήμα που καθορίζει τον ρυθμό είναι το (α) τότε ο ρυθμός παραγωγής οξιρανίου εξαρτάται από την συγκέντρωση του O2 με συνάρτηση της μορφής f(x)=c√ x
(c σταθερά).
-
Κατά την σύνθεση του θειικού οξέος, κεντρικό ρόλο έχει η οξείδωση του SO2 με καταλύτη V2O5. (α) Γράψτε την αντίδραση SO2 και O2 προς SO3. (β) Δώστε μια έκφραση για τον ρυθμό πραγωγής SO3 σαν συνάρτηση των μερικών πιέσεων των αερίων.
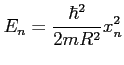 .
.
 Στο διπλανό σχήμα, η διαφορά στην ενέργεια της δεξιάς και αριστερής επιφάνειας (ίδιο υλικό, ίδιο εμβαδόν κάτοψης) είναι EsL, όπου Es η ενέργεια σκαλοπατιού.
(α) Εκτιμήστε την τάξη μεγέθους της ενέργειας σκαλοπατιού σε μέταλλα και για μονοατομικό σκαλοπάτι, δηλαδή με ύψος μόλις ενός ατόμου. (β) Εξηγήστε γιατί η ενέργεια μονοατομικού σκαλοπατιού εξαρτάται και από το υλικό αλλά και από τον προσανατολισμό του σκαλοπατιού πάνω στην επιφάνεια.
Στο διπλανό σχήμα, η διαφορά στην ενέργεια της δεξιάς και αριστερής επιφάνειας (ίδιο υλικό, ίδιο εμβαδόν κάτοψης) είναι EsL, όπου Es η ενέργεια σκαλοπατιού.
(α) Εκτιμήστε την τάξη μεγέθους της ενέργειας σκαλοπατιού σε μέταλλα και για μονοατομικό σκαλοπάτι, δηλαδή με ύψος μόλις ενός ατόμου. (β) Εξηγήστε γιατί η ενέργεια μονοατομικού σκαλοπατιού εξαρτάται και από το υλικό αλλά και από τον προσανατολισμό του σκαλοπατιού πάνω στην επιφάνεια. Υπολογίστε την πλήρωση (f=εμβαδόν ατόμων διά συνολικό εμβαδόν) για την επιφάνεια (110) δομής (α) ClCs και (β) NaCl. Θεωρήστε ότι και στις δυο δομές, τα άτομα είναι ίσες σφαίρες που εφάπτονται.
Υπολογίστε την πλήρωση (f=εμβαδόν ατόμων διά συνολικό εμβαδόν) για την επιφάνεια (110) δομής (α) ClCs και (β) NaCl. Θεωρήστε ότι και στις δυο δομές, τα άτομα είναι ίσες σφαίρες που εφάπτονται.
 Σε ένα πείραμα βρέθηκε ότι νανοσωμάτια Ag τα οποία είχαν αφεθεί να
φτιάξουν το σχήμα ελάχιστης ενέργειας, είχαν σχήμα όπως αυτό της διπλανής
εικόνας. Τι συμπεράσματα μπορείτε να βγάλετε για τις επιφανειακές τάσεις του
αργύρου;
Σε ένα πείραμα βρέθηκε ότι νανοσωμάτια Ag τα οποία είχαν αφεθεί να
φτιάξουν το σχήμα ελάχιστης ενέργειας, είχαν σχήμα όπως αυτό της διπλανής
εικόνας. Τι συμπεράσματα μπορείτε να βγάλετε για τις επιφανειακές τάσεις του
αργύρου;
 Κάποιο μέταλλο φτιάχνει κρυσταλλική δομή με κυβική συμμετρία. Η επιφάνεια (100) έχει τη χαμηλότερη επιφανειακή τάση, και η (111) έχει επιφανειακή τάση μεγαλύτερη κατά 40%, δηλαδή γ111=1.4γ100. Όλες οι άλλες έδρες (hkl) μπορούν να αγνοηθούν. Το σχήμα δείχνει ένα νανοσωματίδιο αυτού του μετάλλου (Α=κέντρο έδρας, Β=μέσον ακμής, C=κορυφή).
Υπολογίστε το λόγο AB/AC.
Κάποιο μέταλλο φτιάχνει κρυσταλλική δομή με κυβική συμμετρία. Η επιφάνεια (100) έχει τη χαμηλότερη επιφανειακή τάση, και η (111) έχει επιφανειακή τάση μεγαλύτερη κατά 40%, δηλαδή γ111=1.4γ100. Όλες οι άλλες έδρες (hkl) μπορούν να αγνοηθούν. Το σχήμα δείχνει ένα νανοσωματίδιο αυτού του μετάλλου (Α=κέντρο έδρας, Β=μέσον ακμής, C=κορυφή).
Υπολογίστε το λόγο AB/AC.



 Κάποιο μέταλλο ατομικού βάρους ΑΒ και πυκνότητας ρ φτιάχνει νανοσωματίδια με σχήμα κόλουρου οκταέδρου, όπως στο διπλανό σχήμα. Το πολύεδρο αυτό έχει 14 έδρες (6 τετράγωνα και 8 εξάγωνα), 36 ακμές, όλες ίσες με α, και 24 κορυφές. Δίνονται οι τύποι για τον όγκο και το συνολικό εμβαδόν.
Oι αποστάσεις των τετράγωνων και εξαγωνικών εδρών από το κέντρο είναι
d1= √2 α και
d2= √6/2 α, αντίστοιχα.
(α) Τι μπορείτε να συνάγετε για τις επιφανειακές τάσεις των επιφανειών του μετάλλου;
(β) Υπολογίστε την ειδική επιφάνεια (συνολικό εμβαδόν δια συνολική μάζα).
(γ) Σε κάποια εφαρμογή είναι ενεργά μόνο τα άτομα των ακμών μεταξύ τετραγώνων και εξαγώνων. Υπολογίστε την συγκέντρωση ενεργών θέσεων (mol ενεργών θέσεων δια συνολική μάζα). Θεωρήστε ότι η διάμετρος του ατόμου είναι D, με D3=ΑΒ/(ρΝΑ).
Κάποιο μέταλλο ατομικού βάρους ΑΒ και πυκνότητας ρ φτιάχνει νανοσωματίδια με σχήμα κόλουρου οκταέδρου, όπως στο διπλανό σχήμα. Το πολύεδρο αυτό έχει 14 έδρες (6 τετράγωνα και 8 εξάγωνα), 36 ακμές, όλες ίσες με α, και 24 κορυφές. Δίνονται οι τύποι για τον όγκο και το συνολικό εμβαδόν.
Oι αποστάσεις των τετράγωνων και εξαγωνικών εδρών από το κέντρο είναι
d1= √2 α και
d2= √6/2 α, αντίστοιχα.
(α) Τι μπορείτε να συνάγετε για τις επιφανειακές τάσεις των επιφανειών του μετάλλου;
(β) Υπολογίστε την ειδική επιφάνεια (συνολικό εμβαδόν δια συνολική μάζα).
(γ) Σε κάποια εφαρμογή είναι ενεργά μόνο τα άτομα των ακμών μεταξύ τετραγώνων και εξαγώνων. Υπολογίστε την συγκέντρωση ενεργών θέσεων (mol ενεργών θέσεων δια συνολική μάζα). Θεωρήστε ότι η διάμετρος του ατόμου είναι D, με D3=ΑΒ/(ρΝΑ).
 Νανοσωματίδια Fe έχουν σχήμα εξαγωνικής ράβδου μήκους L, ενώ η πλευρά του εξαγώνου είναι a=10.2 nm. Σε κάποια εφγαρμογή κατάλυσης, είναι ενεργά μόνο τα άτομα των ακμών του νανοσωματιδίου. Η διάμετρος ενός ατόμου Fe είναι D=0.25 nm και το ατομικό βάρος του Fe είναι A=55.8 g/mol. Υπολογίστε την συγκέντρωση ενεργών θέσεων, nact σε mol/g για L=50 nm και L=200 nm.
Νανοσωματίδια Fe έχουν σχήμα εξαγωνικής ράβδου μήκους L, ενώ η πλευρά του εξαγώνου είναι a=10.2 nm. Σε κάποια εφγαρμογή κατάλυσης, είναι ενεργά μόνο τα άτομα των ακμών του νανοσωματιδίου. Η διάμετρος ενός ατόμου Fe είναι D=0.25 nm και το ατομικό βάρος του Fe είναι A=55.8 g/mol. Υπολογίστε την συγκέντρωση ενεργών θέσεων, nact σε mol/g για L=50 nm και L=200 nm.
 H διπλανή εικόνα δείχνει άτομα της επιφάνειας Pt(111). Άτομα H προσροφώνται στην επιφάνεια και σχηματίζουν περιοδική υπερδομή.
Σημειώστε τις θέσεις των ατόμων H και τα διανύσματα βάσης ώστε η υπερδομή να έχει
H διπλανή εικόνα δείχνει άτομα της επιφάνειας Pt(111). Άτομα H προσροφώνται στην επιφάνεια και σχηματίζουν περιοδική υπερδομή.
Σημειώστε τις θέσεις των ατόμων H και τα διανύσματα βάσης ώστε η υπερδομή να έχει

 Το σχήμα δείχνει καμπύλες μοριακής προσρόφησης αιθανίου, μεθανίου και μιγμάτων τους σε ενεργό άνθρακα. Θεωρήστε ότι το φαινόμενο περιγράφεται με την εξίσωση του Langmuir, N/N∞=KP/(1+KP), όπου
N∞ η οριακή τιμή του N για άπειρη πίεση.
Το σχήμα δείχνει καμπύλες μοριακής προσρόφησης αιθανίου, μεθανίου και μιγμάτων τους σε ενεργό άνθρακα. Θεωρήστε ότι το φαινόμενο περιγράφεται με την εξίσωση του Langmuir, N/N∞=KP/(1+KP), όπου
N∞ η οριακή τιμή του N για άπειρη πίεση.
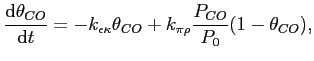 με θCO(0)=0.
Yπολογίστε το θCO σα συνάρτηση του χρόνου. Βρείτε το όριο για t→∞ και σχολιάστε το.
(β) Υπολογίστε, στην ταυτόχρονη ισορροπία των (1) και (2), τα ποσοστά επικάλυψης σαν συνάρτηση των μερικών πιέσεων και των σταθερών ισορροπίας.
με θCO(0)=0.
Yπολογίστε το θCO σα συνάρτηση του χρόνου. Βρείτε το όριο για t→∞ και σχολιάστε το.
(β) Υπολογίστε, στην ταυτόχρονη ισορροπία των (1) και (2), τα ποσοστά επικάλυψης σαν συνάρτηση των μερικών πιέσεων και των σταθερών ισορροπίας.

