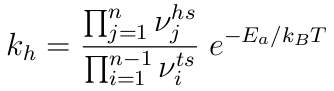Τμήμα Επιστήμης και Τεχνολογίας Υλικών Πανεπιστημίου Κρήτης

Υπολογιστική Επιστήμη Υλικών II: Εργαστήριο Ηλεκτρονικής Δομής (ETY 512)

Γενικές πληροφορίες για το εργαστήριο

Οι παρουσίες στο εργαστήριο είναι υποχρεωτικές. Επιτρέπεται το πολύ μια δικαιολογημένη απουσία. Θα γράψετε αναφορές για τα υπολογιστικά πειράματα που θα εκτελείτε. και για αυτό να έχετε μαζί σας τετράδιο και να κρατάτε αναλυτικές σημειώσεις.

Στο εργαστήριο χρησιμοποιούμε το υπολογιστικό πακέτο ASE (Atomic Simulation Environment), το οποίο είναι πακέτο ανοιχτού κώδικα (GPL) που γράφεται από τους ανθρώπους του CAMD. Είναι γραμμένο σε γλώσσα python. Οι υπολογισμοί με DFT (Density Functional Theory) εκτελούνται από το πρόγραμμα dacapo (από την ίδια ομάδα, επίσης GPL, γραμμένο σε fortran και C).

Μπορείτε, αν θέλετε, να κατεβάσετε τους κώδικες ακολουθώντας τις οδηγίες στις σελίδες του ASE και του dacapo.

Πρίν ξεκινήσετε:

• Διαβάστε για την θεωρία DFT. Δείτε πχ. το κεφ. 2 (σελ. 9-14) της διατριβής του Γ. Α. Τριτσάρη.
• Διαβάστε για το περιβάλλον Linux και γλώσσα προγραμματισμού Python. Δείτε πχ τη σχετική σελίδα του ASE.
• Ανοίξτε ένα terminal. Συνδεθείτε στο cluster της ομάδας θεωρίας υλικών (user βάλτε το username σας),
  

  ssh -X user@mst-0a.cl.materials.uoc.gr

• Ποτέ μην τρέχετε προγράμματα που παίρνουν πάνω από 1-2 λεπτά στο mst-0a. Στέλνετε το πρόγραμμά σας για εκτέλεση με την εντολή
  

   qsub a.out 

  Βλέπετε τι τρέχει με την εντολή
  

   qstat 

  Αν θέλετε να μην τρέξει κάποιο πρόγραμμα, το σκοτώνετε βρίσκοντας τον αριθμό του (πχ 173) από την προηγούμενη εντολή και μετά δίνετε
  

   qdel 173 

• Για να δείτε τα αρχεία σας, πατήστε στο "connect to server", και επιλέξτε σύνδεση ssh και server τον mst-0a.cl.materials.uoc.gr

Ασκήσεις

Οι παρακάτω ασκήσεις θα πρέπει να περιλαμβάνονται στις αναφορές των εργαστηρίων. Οι περισότερες χρησιμεύουν και σαν οδηγοί για τη συγγραφή των αναφορών.

1. 1. Περιγράψτε σύντομα τις φυσικές προσεγγίσεις που εμπεριέχονται σε έναν υπολογισμό με το πρόγραμμα dacapo, ακολουθώντας τα βήματα: 1) πραγματικό υλικό 2) εξίσωση Schrodinger για ηλεκτρόνια 3) εξίσωση Schrodinger για ένα ηλεκτρόνιο 4) μελέτη μόνο ηλεκτρονίων σθένους 5) δυναμικό ανταλλαγής και συσχέτισης.
   2. Ακολουθήστε το παράδειγμα για το μόριο CO. Αντιγράψτε το αρχείο co.py και τρέξτε το με την εντολή
      

      qsub co.py

      Δείτε τα αποτελέσματα στο αρχείο με επέκταση .txt. Στη συνέχεια, δώστε την εντολή

      ag CO.nc
      

      Τι παρατηρείτε; Εξετάστε πώς αλλάζει η ενέργεια του CO καθώς αλλάζει το cell. Πόσο μεγάλο κουτί απαιτείται για να έχετε την ενέργεια με ακρίβεια πρώτου δεκαδικού ψηφίου; Τι θα άλλαζε αν το μόριο δεν ήταν πολικό (πχ O₂);
   3. Εξηγείστε τι είναι η παράμετρος planewavecutoff. Επαναλάβετε τον παραπάνω υπολογισμό για διάφορες τιμές του planewavecutoff (300, 330, 360, ... eV). Πόση είναι η τιμή του για να βρείτε την ενέργεια με ακρίβεια πρώτου δεκαδικού ψηφίου;
   4. Προσθέστε τις παρακάτω εντολές στο πρόγραμμά σας για να βρείτε το μήκος του δεσμού στο CO (δείτε και το παράδειγμα). Αλλάξτε και τα ονόματα των αρχείων στον ορισμό του calc.

      calc.SaveMemory(True)
      calc.StayAliveOn()
      from ASE.Dynamics.QuasiNewton import QuasiNewton
      dyn = QuasiNewton(atoms, fmax=0.05)
      dyn.Converge()
      
      print "atom positions, energy"
      print atoms.GetCartesianPositions(), atoms.GetPotentialEnergy()
      

   5. Τροποποιήστε κατάλληλα το πρόγραμμα plotwavefunction για να δείτε τις κυματοσυναρτήσεις στο μόριο CO, px:

      python -i CO_wavefunction.py 2
      

      Βεβαιωθείτε ότι ταιριάζουν με αυτές που προβλέπει η θεωρία μοριακών τροχιακών. Δείτε και το πρόγραμμα.
   6. Επαναλάβετε τους υπολογισμούς και για άλλα μόρια της επιλογής σας, (πχ O₂, HCl, NH₃, ...). Χρησιμοποιήστε τις ίδιες υπολογιστικές παραμέτρους που βρήκατε για το CO. Βρείτε τα μοριακά τροχιακά.
   7. Xρησιμοποιήστε τα αποτελέσματά σας για να υπολογίσετε αν είναι ενδόθερμες ή εξώθερμες απλές αντιδράσεις (πχ η H₂+½O₂→H₂O). Υπολογίστε την ενθαλπία της αντίδρασης (H=U+PV) σε ΚΣ, θεωρώντας ότι έχουμε τέλειο αέριο. Περιγράψτε πώς θα υπολογίζατε την ελεύθερη ενέργεια της αντίδρασης (G=H-TS).

   ---

2. 1. Ακολουθήστε την άσκηση για να υπολογίσετε την πλεγματική σταθερά και το μέτρο ελαστικότητας του Al.
   2. Επαναλάβετε τον υπολογισμό για μια υποθετική δομή bcc του Al, και βρείτε τη διαφορά ενέργειας μεταξύ των δυο δομών.
   3. Εξηγείστε τι είναι η LDA και τι η GGA. Βρείτε πώς επηρεάζεται η παραπάνω διαφορά από τις διαφορετικές προσεγγίσεις στο δυναμικό ανταλλαγής και συσχέτισης (βάλτε στη συνάρτηση Dacapo όρισμα xc='LDA' ή 'PBE'. default είναι το Pw91). Βρείτε ποια προσέγγιση δίνει καλύτερο αποτέλεσμα σε σχέση με το πείραμα (1.3 kJ/mol).
   4. Υπολογείστε πώς εξαρτώνται από τη συγκεντρωση χ οι ιδιότητες ενός από τα παρακάτω κράμματα:
      • Al-Ni
      • Al-Ti
      • Au-Cu
      • Fe-Pt (Pt-fcc, FePt3-L12, FePt2-C15, FePt-L11, Fe2Pt-C15, Fe3Pt-DO3, Fe-bcc, δείτε εδώ για τις δομές)
      • Si-Ge (Si-A4, Si3Ge-DO3, SiGe-C20 με χ1=0 και χ2=¼, SiGe3-DO3, Ge-A4)
      Ακολουθήστε τα εξής βήματα:
      1. Για το κράμα AB, βρείτε το planewavecutoff και τον αριθμό k-points ώστε να είστε σίγουροι για την ενέργεια στο πρώτο δεκαδικό ψηφίο. Στα άλλα κράμματα A_χB_1-χ να χρησιμοποιήσετε το ίδιο planewavecutoff και αντιστρόφως ανάλογα k-points (L*n=L'*n'), χωρίς να αλλάξετε από άρτιο σε περιττό αριθμό ή το αντίστροφο.
      2. Για κάθε ένα από τα κράματα, ακολουθήστε το παραπάνω παράδειγμα του Al για να βρείτε τις πλεγματικές σταθερές. Σε περιπτώσεις που οι παράμετροι είναι πολλές, κρατήστε τους λόγους σταθερούς και μεταβάλλετε μόνο μία από αυτές.
      3. Βρείτε την πυκνότητα (σε gr/cc), το μέτρο ελαστικότητας (σε GPa), τις αποστάσεις μεταξύ πρώτων γειτόνων, την ενθαλπία σύνθεσης (χA+(1-χ)B→A_χB_1-χ+ΔΗ) και ό,τι άλλο θέλετε.
      4. Δώστε γραφικές παραστάσεις όπου χρειάζεται. Σχολιάστε τυχούσες αποκλίσεις από τον νόμο του Vegard, σύμφωνα με τον οποίο οι ιδιότητες των κραμμάτων A_χB_1-χ είναι γραμμικές συναρτήσεις του χ. Συγκρίνετε αν θέλετε με τη βάση δεδομένων του CAMD.

   ---

3. Ακολουθήστε την άσκηση για να μελετήσετε τις επιφάνειες Al(100) και Al(111) και να υπολογίσετε την επιφανειακή τάση τους και ενέργειες προσρόφησης ατόμων και μορίων.
   1. Χρησιμοποιείστε τα προγράμματα Build.py και Al100.py. Α Υπολογίστε την επιφανειακή τάση με γραφική παράσταση της ενέργειας σαν συνάρτηση του Ν. Βάλτε το πρόγραμμα στο background:

      qsub Al100.py
      

      ή

      python Al100.py &
      

      Όσο τρέχει το πρόγραμμα (20-30 λεπτά), τρέξτε το Build.py και βεβαιωθείτε ότι πρόκειται για σωστή δομή.
   2. Προσθέστε στην βιβλιοθήκη Build.py μια συνάρτηση FCC111. Φτιάξτε ένα πρόγραμμα Al111.py που να την χρησιμοποιεί στα πρότυπα του Al100.py.
   3. Υπολογίστε τις ενέργειες προσρόφησης H και CO στην Al(111). Η ενέργεια προσρόφησης ορίζεται ως Eads=E(X+Al)-E(Al)-E(X). Για το Η πάρτε E(H)=0.5*E(H2). Προσέξτε ώστε όλοι οι υπολογισμοί να γίνουν με τις ίδιες παραμέτρους. Τρέξτε το co@al111.py που υπολογίζει την ενέργεια και τις συντεταγμένες CO προσροφημένου on top στην Al(111). Μετά τροποποιήστε το ώστε να προσομοιώσετε προσρόφηση Η σε θέση fcc hollow (δηλαδή εκεί όπου θα έμπαινε το επόμενο άτομο Al αν το υλικό συνεχιζόταν και πάνω από την επιφάνεια). Δώστε τα μήκη των δεσμών Al-H, Al-C και C-O και συγκρίνετε με το μόριο CO.
   4. Bρείτε τί ποσοστό της επιφάνειας θα καλύπτεται από CO και τι από H σε διάφορες συνθήκες. Χρησιμοποιήστε το μοντέλο του Langmuir:

      H2+2*↔2H*	(1)	(PH2/P) θ*θ*=K1θHθH
      CO+*↔CO*	(2)	(PCO/P) θ*=K2θCO

      Οι σταθερές χημικής ισορροπίας δίνονται από την K=K₀exp(Eads/kT). Πάρτε K₀=10^-5. P είναι η συνολική πίεση, ενώ P_CO και P_H2 είναι οι μερικές πιέσεις. Θεωρήστε ότι P_H2+P_CO=P. To θ συμβολίζει το ποσοστό της επιφάνειας που καλύπτεται από μόρια CO ή H ή είναι κενό (*). Ενδιαφέρουν ιδιαίτερα συνθήκες αποθήκευσης υδρογόνου (λιγότερο από 1 ppm CO, χαμηλή θερμοκρασία). Δώστε τις γραφικές παραστάσεις των θ σαν συνάρτηση της συγκέντρωσης CO και σαν συνάρτηση της θερμοκρασίας. Δείτε το coverage.py.

4. ---

   Σε αυτό το εργαστήριο θα δούμε χαρακτηριστικές τεχνικές μελέτης της ηλεκτρονικής δομής ενός υλικού: την προσομοίωση σαρωτικού μικροσκοπίου σήραγγας (STM), τον υπολογισμό της δομής ζωνών (band structure) και την πυκνότητα καταστάσεων. Θα χρειαστούμε τα αρχεία

   Al-fcc-single.nc 
   al111_3.nc
   h@al111_3.nc 
   co@al111_3.nc 
   

   από τα εργαστήρια 2 και 3.
   1. Περιγράψτε σύντομα την αρχή λειτουργίας του STM. Χρησιμοποιήστε το stm.py για να δείτε προσομοίωση STM από την Al(111).
   2. Πάρτε τρεις εικόνες STM: Τοποθετήστε στην επιφάνειά σας ένα άτομο O σε θέση fcc hollow, με Δz=0.7 Α, όπως παρατηρείται πειραματικά στο άρθρο. Προσομοιώστε την εικόνα STM και συγκρίνετε με το πείραμα (εικ. 2 και 5). Επαναλάβετε τον υπολογισμό με Η στη θέση του Ο. Τι παρατηρείτε;
   Η κίνηση ενός ηλεκτρονίου σε περιοδικό στερεό χαρακτηρίζεται από 4 κβαντικούς αριθμούς, τρεις συνεχείς και ένα θετικό ακέραιο. Οι τρεις συνεχείς αριθμοί είναι οι συνιστώσες του κυματανύσματος k=(k_x, k_y, k_z). Ο ακέραιος αριθμός αριθμεί τα ενεργειακά επίπεδα που αντιστοιχούν σε κάθε τιμή του k. Η εξάρτηση της ενέργειας της ζώνης από τους κβαντικούς αριθμούς λέγεται δομή της ζώνης (band structure). Οι ενέργεια του ηλεκτρονίου είναι περιοδική συνάρτηση του k, δηλαδή Ε(k)=Ε(k+G), όπου G οποιοδήποτε διάνυσμα του αντιστρόφου πλέγματος. Επομένως αρκεί να μελετήσουμε την εξάρτηση της Ε από το k στη θεμελιώση κυψελίδα του αντιστρόφου πλέγματος. Η περιοχή αυτή λέγεται ζώνη Brillouin. Επειδή είναι αδύνατο να σχεδιάσουμε μια συνάρτηση τεσσάρων μεταβλητών, συνήθως ζωγραφίζουμε την E σαν συνάρτηση του μέτρου του k, κατά μήκος συγκεκριμένων κατευθύνσεων της ζώνης Brillouin. Κάποιες δομές ζώνης και τους ορισμούς των σημείων της ζώνης Brillouin μπορείτε να βρείτε εδώ.
   3. Χρησιμοποιήστε την βιβλιοθήκη bstr.py και το πρόγραμμα al_bstr.py για να υπολογίσετε τη δομή ζώνης του Al κατά μήκος των γραμμών WΓ και ΓX. Προσθέστε τις κατευθύνσεις LK, KW, XW και συγκρίνετε με το αποτέλεσμα του παραπάνω αρχείου.
   4. Σχεδιάστε την πυκνότητα καταστάσεων του Al με το dos.py. Κορυφές στην πυκνότητα καταστάσων συδυάζονται με σχετικά επίπεδες μπάντες, ενώ τα ελάχιστα της πυκνότητας καταστάσεων βρίσκονται εκεί όπου οι μπάντες είναι απότομες. Γιατί; Ταυτοποιήστε τέτοια σημεία. Μοιάζει το αποτέλεσμα με την θεωρία ελευθέρων ηλεκτρονίων;
   5. Χρησιμοποιήστε το al_wavefunction.py για να σχεδιάσετε την κυματοσυνάρτηση της χαμηλότερης κατάστασης στο Al. Πώς μοιάζει; Πώς μοιάζουν οι επόμενες (για k=0); ξεχωρίζουν οι αντιδεσμικές;
   6. Υπολογίστε την δομή ζώνης στο Si (LΓXUKΓ) και συγκρίνετε με άλλους υπολογισμούς(άσκηση και εδώ.). Υπολογίστε την πυκνότητα καταστάσεων και σχολιάστε τη σχέση της με τη δομή ζώνης. Σχεδιάστε τις κυματοσυναρτήσεις και συγκρίνετε με την θεωρία LCAO

5. ---

   1. H DFT μπορεί να χρησιμοποιηθεί για τον υπολογισμό των συχνοτήτων δόνησης των μορίων. Υπολογίστε τη δονητική συχνότητα ταλάντωσης τού διατομικού μορίου CO από την σταθερά δύναμης χρησιμοποιώντας τη διαφορά ενέργειας για μικρές απομακρύνσεις από τη θέση ισορροπίας. Θα χρειαστεί να χρησιμοποιήσετε το αποτέλεσμα της άσκησης (1.4). Συγκρίνετε με την πειραματική τιμή και σχολιάστε τυχόν αποκλίσεις. Γιατί τα διατομικά μόρια έχουν ένα κανονικό τρόπο ταλάντωσης (stretching mode); Ποιό είναι το φυσικό νόημα της συχνότητας που υπολογίζετε;
   2. Χρησιμοποιείστε το πρόγραμμα CO_vibrations.py για να βρείτε την δονητική συχνότητα του CO. Συγκρίνετε με την πειραματική τιμή.
   3. Επαναλάβετε τις (1) και (2) για άλλα διατομικά μόρια, όπως για παράδειγμα τα NO, HF, HCl, HBr.
   4. Γράψτε πρόγραμμα στο οποίο να τοποθετείτε ένα μόριο νερού σε κυβικό κουτί (π.χ. ακμής 6 Angstrom). Μπορείτε να χρησιμοποιήσετε σαν αρχικές συντεταγμένες των ατόμων (0,0,0) για το Ο και (-0.77,0,-0.6), (0.77,0,-0.6) για τα άτομα Η. Βρείτε τις θέσεις ισορροπίας όπως κάνατε για το μόριο CO. Στη συνέχεια, εκτελέστε το πρόγραμμα H2O_vib.py. Πόσες δονητικές συχνότητες βρίσκετε και γιατί; Συγκρίνετε τις τιμές των συχνοτήτων με τις πειραματικές τιμές και σχολιάστε τα αίτια πιθανών αποκλίσεων.
   5. Για να δείτε πώς κινούνται τα άτομα με τους κανονικούς τρόπους ταλάντωσης, χρησιμοποιείστε την εντολή plottrajectory και τα αρχεία H2O_vib_mode_x.traj (όπου x είναι ο αριθμός του τρόπου ταλάντωσης με την σειρά που τυπώνεται η συχνότητά του). Χρησιμοποιώντας VMD μπορείτε να δείτε τις κινήσεις των ατόμων σε μορφή "ταινίας". Αφού πάρετε τις πληροφορίες σε αρχεία .xyz με την εντολή

      trajectory2xyz [traj filename] [xyz filename]
      

      Για να δείτε την κίνηση του μορίου, δώστε

      vmd filename.xyz
      

   6. Επαναλάβετε τις (4) και (5) για άλλα πολυατομικά μόρια, όπως π.χ. NH3, CO2, ONF, HCN, OCS, CH4.
   7. Η DFT μπορεί να περιγράψει τον μαγνητισμό των ηλεκτρονίων στα στερεά. Η μέθοδος Spin-polarized Density Functional Theory, εκτός από τον ποσοτικό καθορισμό μαγνητικών ροπών σπιν, προσφέρει και στην κατανόηση των βασικών μηχανισμών μαγνητισμού στα στερεά. Στην άσκηση αυτή μελετάμε μεταβατικά μέταλλα (Fe, Co, Ni) σαν παραδείγματα στα οποία η DFT προβλέπει και ερμηνεύει μαγνητικές ιδιότητες. Ακολουθείστε την άσκηση για να μελετήσετε τον Fe (δομή bcc).
   8. Επαναλάβετε για άλλα μέταλλα.

6. ---

   1. Σε αυτό το εργαστήριο μελετάμε την κίνηση ατόμου προσροφημένου σε επιφάνεια. Η διάχυση ατόμων σε επιφάνειες, εκτός από το θεμελιώδες της ενδιαφέρον, σχετίζεται με φαινόμενα και διεργασίες μεγάλης τεχνολογικής σημασίας, όπως είναι η μοριακή επιταξία και η κατάλυση. Ακολουθήστε την άσκηση για να μελετήσετε τους μηχανισμούς αυτο-διάχυσης πάνω στην επιφάνεια Al(110). Βρέστε τις διαδρομές ελάχιστης ενέργειας και τις μεταβατικές καταστάσεις με την μέθοδο "Nudged Elastic Band" για τις τρεις διεργασίες που περιγράφονται στην άσκηση και συγκρίνετε τα αντίστοιχα φράγματα ενέργειας.
   2. Για τον υπολογισμό του ρυθμού αναπήδησης (hopping rate) των ατόμων, k , από ένα σημείο ελάχιστης ενέργειας της επιφάνειας σε άλλο χρησιμοποιείται η θεωρία μεταβατικής κατάστασης (transition state theory), που στην απλούστερη αρμονική προσέγγιση δίνει k=ν₀e^-E_a/k_BT. όπου E_a είναι το φράγμα ενέργειας και ν₀ είναι η συχνότητα ταλάντωσης του προσροφημένου ατόμου γύρω από το σημείο ισορροπίας (ελάχιστης ενέργειας). Χρησιμοποιώντας την παραπάνω σχέση, σχεδιάστε την γραφική παράσταση k vs 1/k_BT για τις διεργασίες που μελετήσατε παραπάνω.
   3. Ακολουθήστε την άσκηση που προσεγγίζει (αναλυτικά) την διάχυση ατόμου υδρογόνου προσροφημένου σε μεταλλική επιφάνεια. Για τον υπολογισμό του ρυθμού αναπήδησης χρησιμοποιήστε το αποτέλεσμα της αρμονικής θεωρίας μεταβατικής κατάστασης, όπου ν_j^hs είναι οι τρείς συχνότητες στο σημείο ισορροπίας και ν_i^ts είναι οι δύο συχνότητες στην μεταβατική κατάσταση.